Question

【题目】已知函数f（x）= 在点（1，f（1））处的切线与x轴平行．
（1）求实数a的值及f（x）的极值；
（2）若对任意x1 ， x2∈[e2 ， +∞），有| |＞ ，求实数k的取值范围．

Answer 1

【答案】
（1）解：∵函数f（x）= ，

∴ ，

令f'（1）=0，

∴ =0，

解得a=1；

令f′（x）=0，则lnx=0，

解得x=1，

即f（x）有极大值为f（1）=1

（2）解：由| |＞ ，可得 ，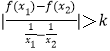

令 ，则g（x）=x﹣xlnx，其中x∈（0，e﹣2]，

g'（x）=﹣lnx，又x∈（0，e﹣2]，则g'（x）=﹣lnx≥2，

即 ，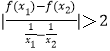

因此实数k的取值范围是（﹣∞，2]

【解析】（1）求函数f（x）的导数，根据导数的几何意义求出a的值，再利用f′（x）=0，求出函数f（x）的极值；（2）由| |＞ 变形得 ，构造函数 ，利用导数求出g（x）在定区间上的取值范围即可．
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识，掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值．