题目内容
13.某空间几何体的三视图如图所示,则此几何体的体积为( )
| A. | 14π | B. | $\frac{10}{3}π$ | C. | $\frac{16}{3}π$ | D. | $\frac{22}{3}π$ |
分析 由已知中的三视图,可知该几何体是一个圆锥挖去一个圆柱所得的组合体,分别求出圆锥和圆柱的体积,相减可得答案.
解答 解:由已知中的三视图,可知该几何体是一个圆锥挖去一个圆柱所得的组合体,
由圆锥的底面直径为4,可得圆锥的底面半径为2,且圆锥的高为4,
故圆锥的体积为:$\frac{1}{3}π{•2}^{2}•4$=$\frac{16π}{3}$,
由圆柱的底面直径为2,可得圆柱的底面半径为1,且圆柱的高为2,
故圆柱的体积为:π•12•2=2π,
故组合体的体积V=$\frac{16π}{3}$-2π=$\frac{10}{3}π$,
故选:B.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
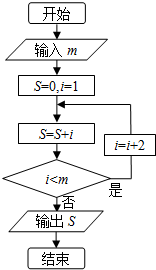
1.阅读如图所示的程序框图,若输入m=6,则输出S等于( )

| A. | 4 | B. | 9 | C. | 16 | D. | 25 |
2.下列不等式中,与不等式$\frac{x+8}{{{x^2}+2x+3}}$<2解集相同的是( )
| A. | (x+8)(x2+2x+3)<2 | B. | x+8<2(x2+2x+3) | C. | $\frac{1}{{{x^2}+2x+3}}$<$\frac{2}{x+8}$ | D. | $\frac{{{x^2}+2x+3}}{x+8}$>$\frac{1}{2}$ |