题目内容
4.不等式${A}_{8}^{x}$<6${A}_{8}^{x-2}$的解集为{8}.分析 根据排列数公式,转化为关于x的不等式,注意x的取值范围.
解答 解:∵${A}_{8}^{x}$<6${A}_{8}^{x-2}$,
∴$\frac{8!}{(8-x)!}$<$\frac{6×8!}{(10-x)!}$,且2≤x≤8,
∴(10-x)(9-x)<6,
解得7<x<12,又2≤x≤8,
∴7<x≤8,
故答案为:{8}.
点评 本题考查了排列数公式和不等式的解法,属于基础题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
16.已知函数f(x)=|x-2|+1,g(x)=loga(x+1)(a>0,且a≠1),若函数f(x)-g(x)有两个不相同的零点,则实数a的取值范围是( )
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,1) | C. | (1,3) | D. | (3,+∞) |
13.某空间几何体的三视图如图所示,则此几何体的体积为( )


| A. | 14π | B. | $\frac{10}{3}π$ | C. | $\frac{16}{3}π$ | D. | $\frac{22}{3}π$ |
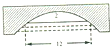 一座圆形拱桥,当水面在如图所示位置时,拱桥离水面2米,水面宽12米,当水面下降1米后水面宽为2$\sqrt{51}$米.
一座圆形拱桥,当水面在如图所示位置时,拱桥离水面2米,水面宽12米,当水面下降1米后水面宽为2$\sqrt{51}$米.