题目内容
13.设函数f(x)=mx2-2mlnx-6+m,g(x)=x2-lnx(1)当m=1时,求函数f(x)的单调区间及极值;
(2)若对于x∈[1,3],f(x)<0恒成立,求实数m的取值范围;
(3)若m>0且对于任意x1∈[1,e],任意x2∈[1,e],不等式f(x1)>g(x2)恒成立,求实数m的取值范围.
分析 (1)求出函数的导数,求得单调区间和极值,注意定义域;
(2)求出f(x)的导数,求得单调区间,求出最大值,由不等式恒成立思想解不等式即可得到m的范围;
(3)求出f(x)的导数,求得f(x)在[1,e]的最大值,求得g(x)的导数,求得g(x)在[1,e]的最小值,由不等式恒成立思想,解不等式即可得到m的范围.
解答 解:(1)当m=1时,函数f(x)=x2-2lnx-5的导数为f′(x)=2x-$\frac{2}{x}$=$\frac{2(x-1)(x+1)}{x}$,
当x∈(0,1)时,f′(x)<0,f(x)递减,当x∈(1,+∞)时,f′(x)>0,f(x)递增,
即有f(x)的增区间为(1,+∞),减区间为(0,1),f(x)的极小值为f(1)=-4,无极大值;
(2)f′(x)=2mx-$\frac{2m}{x}$=$\frac{2m(x-1)(x+1)}{x}$,x>0,
当m=0时,f(x)=-6<0恒成立;
m>0时,x∈[1,3],f′(x)>0,f(x)递增,f(3)取得最大值,且为10m-2mln3-6,
由恒成立,可得f(3)<0即有0<m<$\frac{3}{5-ln3}$;
m<0时,x∈[1,3],f′(x)<0,f(x)递减,f(1)取得最大值,且为2m-6,
由恒成立,可得f(1)<0即有m<3,即有m<0.
综上可得,实数m的取值范围是(-∞,$\frac{3}{5-ln3}$).
(3)m>0由(2)得f(x)在[1,e]上递增,f(x)的最小值f(1)=2m-6,
g′(x)=2x-$\frac{1}{x}$=$\frac{2{x}^{2}-1}{x}$,在[1,e]上g′(x)>0,g(x)递增,g(x)的最大值为g(e)=e2-1.
由任意x1∈[1,e],任意x2∈[1,e],不等式f(x1)>g(x2)恒成立,
即有2m-6>e2-1,解得m>$\frac{{e}^{2}+5}{2}$.
即有m的取值范围是($\frac{{e}^{2}+5}{2}$,+∞).
点评 本题考查导数的运用:求单调区间和极值、最值,主要考查函数的单调性的运用,同时考查不等式恒成立思想的运用,属于中档题.

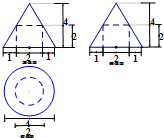
| A. | 14π | B. | $\frac{10}{3}π$ | C. | $\frac{16}{3}π$ | D. | $\frac{22}{3}π$ |
| A. | f(x)=-x3 | B. | f(x)=$\sqrt{-x}$ | C. | f(x)=-tanx | D. | f(x)=$\frac{1}{x}$ |