题目内容
1.已知函数f(x)=$\sqrt{{x}^{2}-4x+8}$+$\sqrt{{x}^{2}-2x+2}$,求f(x)的最小值,并求此时的x的值.分析 化简f(x)=$\sqrt{(x-2)^{2}+4}$+$\sqrt{(x-1)^{2}+1}$,从而可知f(x)是点C(x,0)与点B(2,-2)、A(1,1)的距离之和,从而作图求解即可.
解答 解:f(x)=$\sqrt{{x}^{2}-4x+8}$+$\sqrt{{x}^{2}-2x+2}$=$\sqrt{(x-2)^{2}+4}$+$\sqrt{(x-1)^{2}+1}$,
故f(x)=$\sqrt{{x}^{2}-4x+8}$+$\sqrt{{x}^{2}-2x+2}$是点C(x,0)与点B(2,-2)、A(1,1)的距离之和,如图,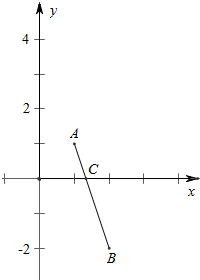
结合图象可知,
当A、B、C三点共线时,f(x)有最小值.
f(x)的最小值为$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$;
此时x=1+$\frac{1}{3}$=$\frac{4}{3}$.
点评 本题考查了数形结合的思想应用及几何意义的应用,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
16.设i是虚数单位,则|(1+i)-$\frac{2}{i}$|=( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |