题目内容
设x1,x2是关于x的一元二次方程x2-2(m-1)x+m+1=0的两个实根,又y=x21+x22,求y=f(m)的解析式及此函数的定义域.
y=f(m)=4m2-10m+2(m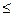 0或m
0或m 3)
3)
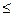 0或m
0或m 3)
3)∵x1,x2是x2-2(m-1)x+m+1=0的两个实根,
∴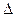 =4(m-1)2-4(m+1)
=4(m-1)2-4(m+1) 0,解得m
0,解得m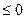 或m
或m 3。
3。
又∵x1+x2=2(m-1), x1·x2=m+1,
∴y=f(m)=x12+x22=(x1+x2)2-2x1x2=4m2-10m+2,
即y=f(m)=4m2-10m+2(m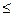 0或m
0或m 3)。
3)。
∴
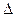 =4(m-1)2-4(m+1)
=4(m-1)2-4(m+1) 0,解得m
0,解得m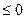 或m
或m 3。
3。又∵x1+x2=2(m-1), x1·x2=m+1,
∴y=f(m)=x12+x22=(x1+x2)2-2x1x2=4m2-10m+2,
即y=f(m)=4m2-10m+2(m
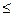 0或m
0或m 3)。
3)。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
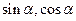 是方程
是方程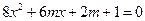 的两个实数根,求实数
的两个实数根,求实数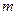 的值.
的值.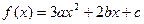 ,若a+b+c=0,f(0)f(1)>0,
,若a+b+c=0,f(0)f(1)>0,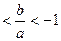 ;
;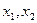 是方程f(x)=0的两个根,求
是方程f(x)=0的两个根,求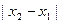 的取值范围
的取值范围
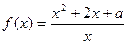
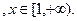 若对任意
若对任意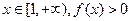 恒成立,试求实数
恒成立,试求实数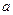 的取值范围。
的取值范围。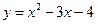 的定义域为
的定义域为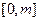 ,值域为
,值域为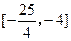 ,则
,则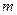 的取值范围是( )
的取值范围是( )
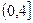
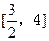
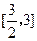
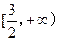
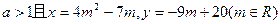 ;则
;则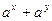 的最小值为 (用
的最小值为 (用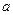 表示)。
表示)。