题目内容
已知定义在R上的函数f(x)满足:f(x)=
,且f(x+2)=f(x),g(x)=
,则方程f(x)=g(x)在区间[-8,3]上的所有实根之和为______.
|
| 2x+5 |
| x+2 |
由f(x+2)=f(x),知f(x)是周期为2的周期函数.
分别作出函数y=f(x)与y=g(x)的图象,如图所示.
这两个函数的图象关于点P(-2,2)中心对称,故它们的交点也关于点P(-2,2)中心对称,
从而方程f(x)=g(x)在区间[-8,3]上的所有6个实根也是两两成对地关于点P(-2,2)中心对称,
则方程f(x)=g(x)在区间[-8,3]上的所有实根之和为3×(-4)=-12.
故答案为:-12.

分别作出函数y=f(x)与y=g(x)的图象,如图所示.
这两个函数的图象关于点P(-2,2)中心对称,故它们的交点也关于点P(-2,2)中心对称,
从而方程f(x)=g(x)在区间[-8,3]上的所有6个实根也是两两成对地关于点P(-2,2)中心对称,
则方程f(x)=g(x)在区间[-8,3]上的所有实根之和为3×(-4)=-12.
故答案为:-12.

练习册系列答案
相关题目


 有两个不相等的实根,且必有一个根属于
有两个不相等的实根,且必有一个根属于
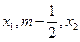 成等差数例,设函数
成等差数例,设函数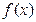 的图象的对称轴为
的图象的对称轴为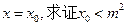 。
。 的反函数为
的反函数为 ,则方程
,则方程 的解
的解 .
. 与函数
与函数 的图象的交点个数为( )
的图象的交点个数为( ) 个
个 个
个 个
个 个
个 的零点所在的区间是 ( )
的零点所在的区间是 ( )