题目内容
【题目】已知下列命题:
①函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②若函数![]() 在
在![]() 上有两个零点,则
上有两个零点,则![]() 的取值范围是
的取值范围是![]() ;
;
③当![]() 时,函数
时,函数![]() 的最大值为0;
的最大值为0;
④函数![]() 在
在![]() 上单调递减;
上单调递减;
上述命题正确的是_________(填序号).
【答案】①②④
【解析】
根据复合函数的单调性即可判断①;令函数![]() ,确定当
,确定当![]() 的图象与直线
的图象与直线![]() 有两个交点时
有两个交点时![]() 的取值范围即可判断②;利用基本不等式求得函数的最大值即可判断③;利用辅助角公式和整体对应法判断正弦型函数的单调性即可判断④;
的取值范围即可判断②;利用基本不等式求得函数的最大值即可判断③;利用辅助角公式和整体对应法判断正弦型函数的单调性即可判断④;
①根据复合函数同增异减的性质,令![]() ,则
,则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,又因为
上单调递增,又因为![]() 为增函数,可知函数
为增函数,可知函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故①正确;
上单调递增,故①正确;
②令![]() ,则函数
,则函数![]() 在
在![]() 上有两个零点等价于函数
上有两个零点等价于函数![]() 的图象与直线
的图象与直线![]() 有两个交点,作图如下:根据函数
有两个交点,作图如下:根据函数![]() 的图象可知
的图象可知![]() ,故②正确;
,故②正确;

③当![]() 时,
时,![]() ,所以
,所以![]()
(当且仅当![]() ,即
,即![]() 时取等号),所以函数
时取等号),所以函数![]() 的最大值为
的最大值为![]() ,故③不正确.
,故③不正确.
④![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,故④正确;
单调递减,故④正确;
故答案为:①②④

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】2020年春季受新冠肺炎疫情的影响,利用网络软件办公与学习成为了一种新的生活方式,网上办公软件的开发与使用成为了一个热门话题.为了解“钉钉”软件的使用情况,“钉钉”公司借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
35岁及以下 | 70 | 30 | 100 |
35岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为“钉钉”软件的使用情况与年龄有关?
(2)现从所抽取的35岁以上的网友中利用分层抽样的方法再抽取5人.从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用“钉钉”软件的概率.
参考公式: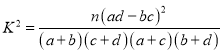 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】已知某快递公司收取快递费的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,在收费
的包裹,在收费![]() 元的基础上,每超过
元的基础上,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了
元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了![]() 件这种包裹的两个统计数表如下:
件这种包裹的两个统计数表如下:
表![]()
包裹重量 |
|
|
|
|
|
包裹数 |
|
|
|
|
|
损坏件数 |
|
|
|
|
|
表![]()
包裹重量 |
|
|
|
|
|
出厂价(元 |
|
|
|
|
|
卖价(元 |
|
|
|
|
|
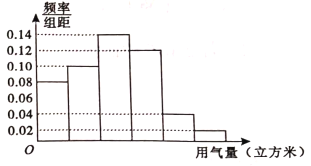
![]() 估计该快递公司对每件包裹收取快递费的平均值;
估计该快递公司对每件包裹收取快递费的平均值;
![]() 将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的
将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的![]() 赔偿给厂家.现该厂准备给客户邮寄重量在区间
赔偿给厂家.现该厂准备给客户邮寄重量在区间![]() 和
和![]() 内的工艺品各
内的工艺品各![]() 件,求该厂家这两件工艺品获得利润的分布列和期望.
件,求该厂家这两件工艺品获得利润的分布列和期望.