Question

【题目】天然气已经进入了千家万户，某市政府为了对天然气的使用进行科学管理，节约气资源，计划确定一个家庭年用量的标准.为此，对全市家庭日常用气的情况进行抽样调查，获得了部分家庭某年的用气量（单位：立方米）.将统计结果绘制成下面的频率分布直方图（如图所示）.由于操作失误，横轴的数据丢失，但可以确定横轴是从0开始计数的.若以各组区间中点值代表该组的取值，则估计全市家庭年均用气量约为（ ）

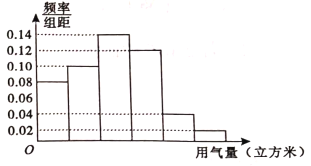
A.6.5立方米B.5立方米C.4.5立方米D.2.5立方米

Answer 1

【答案】B

【解析】

设各小长方形的宽度为，根据各小长方形面积总和为1求出，再由平均数小长方形的面积小矩形底边中点的横坐标之和，即可求解.

设各小长方形的宽度为，

由频率分布直方图中各小长方形面积总和为1可得，

，解得.

各小组依次是，，，，，，

其中点分别是1，3，5，7，9，11，对应的频率分别为0.16，0.20，0.28，0.24，0.08，0.04，

故估计全市家庭年均用气量为：

（立方米）.

故选：B.