题目内容
【题目】已知下列命题:
①函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②若函数![]() 在
在![]() 上有两个零点,则
上有两个零点,则![]() 的取值范围是
的取值范围是![]() ;
;
③当![]() 时,函数
时,函数![]() 的最大值为0;
的最大值为0;
④函数![]() 在
在![]() 上单调递减;
上单调递减;
上述命题正确的是_________(填序号).
【答案】①②④
【解析】
根据复合函数的单调性即可判断①;令函数![]() ,确定当
,确定当![]() 的图象与直线
的图象与直线![]() 有两个交点时
有两个交点时![]() 的取值范围即可判断②;利用基本不等式求得函数的最大值即可判断③;利用辅助角公式和整体对应法判断正弦型函数的单调性即可判断④;
的取值范围即可判断②;利用基本不等式求得函数的最大值即可判断③;利用辅助角公式和整体对应法判断正弦型函数的单调性即可判断④;
①根据复合函数同增异减的性质,令![]() ,则
,则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,又因为
上单调递增,又因为![]() 为增函数,可知函数
为增函数,可知函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故①正确;
上单调递增,故①正确;
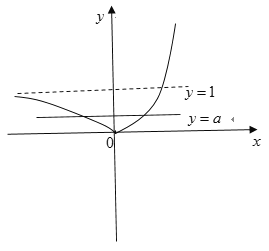
②令![]() ,则函数
,则函数![]() 在
在![]() 上有两个零点等价于函数
上有两个零点等价于函数![]() 的图象与直线
的图象与直线![]() 有两个交点,作图如下:根据函数
有两个交点,作图如下:根据函数![]() 的图象可知
的图象可知![]() ,故②正确;
,故②正确;
③当![]() 时,
时,![]() ,所以
,所以![]()
(当且仅当![]() ,即
,即![]() 时取等号),所以函数
时取等号),所以函数![]() 的最大值为
的最大值为![]() ,故③不正确.
,故③不正确.
④![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,故④正确;
单调递减,故④正确;
故答案为:①②④

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目