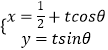Question

【题目】设等差数列{an}满足3a8=5a15 ， 且 ，Sn为其前n项和，则数列{Sn}的最大项为（　　）
A.
B.S24
C.S25
D.S26

Answer 1

【答案】C
【解析】解：设等差数列{an}的公差为d，∵3a8=5a15，∴3（a1+7d）=5（a1+14d），化为2a1+49d=0，

∵ ，∴d＜0，∴等差数列{an}单调递减，

Sn=na1+ d= + d= （n﹣25）2﹣ d．

∴当n=25时，数列{Sn}取得最大值，

故答案为：C．

由于该数列为等差数列，且满足3a8=5a15，化解后可得2a1+49d=0，不难判断出 a 1 > 0 ，d＜0，结合等差数列的前n项和公式可得n=25时，数列{Sn}取得最大值.