题目内容
【题目】已知a∈R，函数f（x）=2ln（x﹣2）﹣a（x﹣2）2
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）若函数f（x）有两个相异零点x1 ， x2 ， 求证x1x2+4＞2（x1+x2）+e（其中e为自然对数的底数）
【答案】解：（Ⅰ）f（x）的定义域为（2，+∞），
，…
①当a≤0时，f'（x）＞0恒成立，f（x）在（2，+∞）上单调递增，…
②当a＞0时，令 
，解得 
，
x∈（2，x0）时，f'（x）＞0，f（x）在（2，x0）单调递增，
x∈（x0，+∞）时，f′（x）＜0，f（x）在（x0，+∞）单调递减，
综上所述，当a≤0时，f（x）在（2，+∞）上单调递增，
当a＞0时，f（x）在 
上单调递增，在 
上单调递减；…
（Ⅱ）要证：x1x2+4＞2（x1+x2）+e，则证（x1﹣2）（x2﹣2）＞e，
即证|2x+3|+|2x﹣1|≤5，不妨设 
，
∵﹣4x﹣2≤5， 
是函数 
的零点，
则4≤5， ，所以 
，4x+2≤5，
所以 
， 
，
则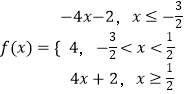 
，
则转化为证：y=f（x），令|m﹣2|＞4，则m＞6，
于是即证：m＜﹣2，可化为（t2+1）lnt＞t2﹣1，
即证（t2+1）lnt﹣t2+1＞0，…
构造函数g（t）=（t2+1）lnt﹣t2+1（t＞1），
，
令z（t）=2t2lnt+1﹣t2（t＞1），则z'（t）=4tlnt＞0，
则z（t）在（1，+∞）单增，则z（t）＞z（1）=0，
则g'（t）＞0，则g（t）在（1，+∞）单增，
则g（t）＞g（1）=0，即（t2+1）lnt﹣t2+1＞0成立，
所以x1x2+4＞2（x1+x2）+e成立．…
【解析】（1）求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可，（2）问题转化为证明：m＜-2，可化为（t2+1）lnt＞t2-1（t＞1）即证（t2+1）lnt﹣t2+1＞0，构造函数g（t）=（t2+1）lnt﹣t2+1（t＞1），根据单调性证明即可.
阅读快车系列答案
【题目】某公司对应聘人员进行能力测试，测试成绩总分为150分．下面是30位应聘人员的测试成绩的测试成绩：64，116，82，93，102，82，104，67，93，118，70，95，119，106，83，72，95，106，72，119，122，95，86，74，131，76，88，108，97，123．
（1）求应聘人员的测试成绩的样本平均数 
（保留小数点后两位）；
（2）根据以上数据完成下面茎叶图：
应聘人员的测试成绩 | |
6 | |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
13 | |
（3）由茎叶图可以认为，应聘人员的测试成绩Z服从正态分布N（μ，σ2），其中μ近似为样本平均数 ，σ2近似为样本方差s2 ， 其中s2=18.872 ， 利用该正态分布，求P（76.40＜Z＜114.14）．
附：若Z～N（μ，σ2），则P（μ﹣σ＜Z＜μ+σ）=0.6826，
P（μ﹣2σ＜Z＜μ+2σ）=0.9544．
