题目内容
【题目】已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=(x+1)ex则对任意的m∈R,函数F(x)=f(f(x))﹣m的零点个数至多有( )
A.3个
B.4个
C.6个
D.9个
【答案】A
【解析】解:当x<0时,f(x)=(x+1)ex,可得f′(x)=(x+2)ex,可知x∈(﹣∞,﹣2),函数是减函数,x∈(﹣2,0)函数是增函数,
f(﹣2)= ![]() ,f(﹣1)=0,且x→0时,f(x)→1,又f(x)是定义在R上的奇函数,f(0)=0,而x∈(﹣∞,﹣1)时,f(x)<0,
,f(﹣1)=0,且x→0时,f(x)→1,又f(x)是定义在R上的奇函数,f(0)=0,而x∈(﹣∞,﹣1)时,f(x)<0,
所以函数的图象如图:令t=f(x)则f(t)=m,
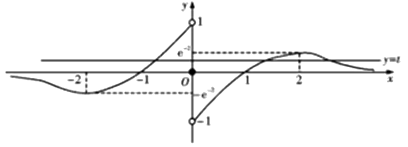
由图象可知:当t∈(﹣1,1)时,方程f(x)=t至多3个根,当t(﹣1,1)时,方程没有实数根,
而对于任意m∈R,方程f(t)=m至多有一个根,t∈(﹣1,1),
从而函数F(x)=f(f(x))﹣m的零点个数至多有3个.
故答案为:A.
当x<0时,f(x)=(x+1)ex,可得f′(x)=(x+2)ex可知x∈(﹣∞,﹣2),函数是减函数,x∈(﹣2,0)函数是增函数,并且f(﹣2)= ![]() ,f(﹣1)=0,且x→0时,f(x)→1,根据f(x)为奇函数,其图像关于原点对称,根据分析结果,作出f(x)的大致图象,数形结合不难得出零点最多为3个.
,f(﹣1)=0,且x→0时,f(x)→1,根据f(x)为奇函数,其图像关于原点对称,根据分析结果,作出f(x)的大致图象,数形结合不难得出零点最多为3个.

【题目】某中学人力资源部计划2016年招聘2名数学教师,共5名应聘者进入最后课堂实录环节.5名数学组评审专家给出评分如表:
评审专家/应聘老师 | 1 | 2 | 3 | 4 | 5 |
评审专家A | 93.0 | 90.0 | 88.5 | 89.5 | 82.5 |
评审专家B | 94.0 | 83.0 | 89.0 | 93.0 | 81.0 |
评审专家C | 91.0 | 85.0 | 81.5 | 88.0 | 81.0 |
评审专家D | 92.0 | 91.5 | 81.0 | 94.5 | 87.0 |
评审专家E | 95.5 | 91.0 | 90.0 | 95.5 | 88.5 |
(Ⅰ)若依据去掉一个最高分和一个最低分规则计算应聘老师成绩,试确定最终应聘成功的2名数学老师的序号;
(Ⅱ)在课堂实录环节,每名应聘老师都需要从5名评审专家中随机选取2名进行点评,且每名应聘老师的选择互不影响,设X表示评审专家A进行点评的次数,求X的分布列以及数学期望;
(Ⅲ)记评审专家A与评审专家B给出的评分的方差分别为 ![]() ,试比较
,试比较 ![]() 与
与 ![]() 的大小.(只需写出结论)
的大小.(只需写出结论)