题目内容
【题目】如图,在三棱台DEF﹣ABC中,AB=2DE,G,H分别为AC,BC的中点.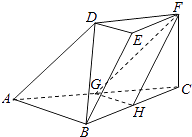
(Ⅰ)求证:BD∥平面FGH;
(Ⅱ)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45°,求平面FGH与平面ACFD所成的角(锐角)的大小.
【答案】解:(Ⅰ)证明:根据已知条件,DF∥AC,EF∥BC,DE∥AB;
△DEF∽△ABC,又AB=2DE,
∴BC=2EF=2BH,
∴四边形EFHB为平行四边形;
∴BE∥HF,HF平面FGH,BE平面FGH;
∴BE∥平面FGH;
同样,因为GH为△ABC中位线,∴GH∥AB;
又DE∥AB;
∴DE∥GH;
∴DE∥平面FGH,DE∩BE=E;
∴平面BDE∥平面FGH,BD平面BDE;
∴BD∥平面FGH;
(Ⅱ)连接HE,则HE∥CF;
∵CF⊥平面ABC;
∴HE⊥平面ABC,并且HG⊥HC;
∴HC,HG,HE三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,设HC=1,则:
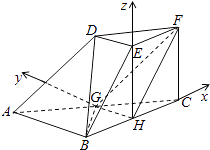
H(0,0,0),G(0,1,0),F(1,0,1),B(﹣1,0,0);
连接BG,根据已知条件BA=BC,G为AC中点;
∴BG⊥AC;
又CF⊥平面ABC,BG平面ABC;
∴BG⊥CF,AC∩CF=C;
∴BG⊥平面ACFD;
∴向量 ![]() 为平面ACFD的法向量;
为平面ACFD的法向量;
设平面FGH的法向量为 ![]() ,则:
,则:
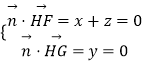 ,取z=1,则:
,取z=1,则: ![]() ;
;
设平面FGH和平面ACFD所成的锐二面角为θ,则:cosθ=|cos ![]() |=
|= ![]() ;
;
∴平面FGH与平面ACFD所成的角为60°.
【解析】(1)根据AB=2DE,可得到BC=2EF,证出EFHB为平行四边形,故BE∥HF,便有BE∥面FGH,再证明DE∥平面FGH,从而得到片BDE∥面FGH,结果得证;(2)连接HE,证明出HC,HG,HE三直线两两垂直,分别以这三直线为x,y,z轴,以H为坐标原点建立空间直角坐标系,由向量法可得平面FGH与平面ACFD所成角的大小.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 名校课堂系列答案
名校课堂系列答案【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量y(g)与尺寸x(mm)之间近似满足关系式y=axb(a,b为大于0的常数).现随机抽取6件合格产品,测得数据如下:
尺寸(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量(g) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
对数据作了初步处理,相关统计量的值如表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)根据所给数据,求y关于x的回归方程;
(Ⅱ)按照某项指标测定,当产品质量与尺寸的比在区间( ![]() ,
, ![]() )内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
)内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
附:对于一组数据(v1 , u1),(v2 , u2),…,(vn , un),其回归直线u=α+βv的斜率和截距的最小二乘估计分别为 ![]() =
= 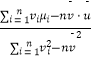 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.