题目内容
8.在直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系.已知曲线C1:$\left\{\begin{array}{l}{x=4+t}\\{y=5+2t}\end{array}\right.$(t为参数),曲线C2:ρ2-6ρcosθ-10ρsinθ+9=0.(Ⅰ)将曲线C1化成普通方程,将曲线C2化成参数方程;
(Ⅱ)判断曲线C1和曲线C2的位置关系.
分析 (Ⅰ)消去参数t,把曲线C1的参数方程化为普通方程;利用极坐标公式,把曲线C2的极坐标方程化为普通方程,再把普通方程化为参数方程;
(Ⅱ)由曲线C1上的点P到圆C2的圆心O′的距离|PO′|<r,得出曲线C1、C2相交.
解答 解:(Ⅰ)∵曲线C1:$\left\{\begin{array}{l}{x=4+t}\\{y=5+2t}\end{array}\right.$,
∴t=x-4,
代入y=5+2t得,
y=5+2(x-4),即y=2x-3.
∴曲线C1的普通方程是y=2x-3;…(2分)
将ρ=$\sqrt{{x}^{2}{+y}^{2}}$,ρcosθ=x,ρsinθ=y代入曲线C2的方程
ρ2-6ρcosθ-10ρsinθ+9=0,得
x2+y2-6x-10y+9=0,…(4分)
即(x-3)2+(y-5)2=25;…(5分)
设x-3=5cosα,y-5=5sinα,
得曲线C2的参数方程:$\left\{\begin{array}{l}{x=3+5cosα}\\{y=5+5sinα}\end{array}\right.$(α为参数);…(6分)
(Ⅱ)由(Ⅰ)知,曲线C1是经过点P(4,5)的直线,
曲线C2是以O′(3,5)为圆心,半径为r=5的圆;…(7分)
∵|PO′|=1<r,…(8分)
∴点P(4,5)在曲线C2内,…(9分)
∴曲线C1和曲线C2相交.…(10分)
点评 本题考查了直线与圆的应用问题,也考查了参数方程与极坐标方程的应用问题,是基础题目.

练习册系列答案
相关题目
18.已知锐角α、β满足cosα=$\frac{3}{5}$,cos(α+β)=-$\frac{5}{13}$,则cosβ=( )
| A. | $\frac{56}{65}$ | B. | $\frac{33}{65}$ | C. | $-\frac{56}{65}$ | D. | $-\frac{33}{65}$ |
16.具有线性相关关系得变量x,y,满足一组数据如表所示,若y与x的回归直线方程为$\widehat{y}$=3x-$\frac{3}{2}$,则m的值( )
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 8 |
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |
20.已知随机变量X服从正态分布N(1,σ2),且P(X≤0)=0.1,则P(X>2)=( )
| A. | 0.9 | B. | 0.1 | C. | 0.6 | D. | 0.4 |
18.下列函数中,既是偶函数又是在区间(-∞,0)上单调递增的函数是( )
| A. | y=ln|x| | B. | y=x2 | C. | y=tanx | D. | y=2-|x| |
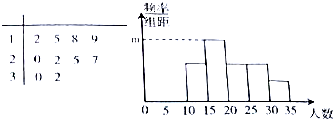 从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))
从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))