题目内容
19.已知a,b,c为直角三角形的三边,其中c是斜边,若$\frac{1}{{a}^{2}}$+$\frac{4}{{b}^{2}}$+$\frac{t}{{c}^{2}}$≥0恒成立,则实数t的取值范围是[-9,+∞).分析 问题转化为:t≥-($\frac{{c}^{2}}{{a}^{2}}$+$\frac{{4c}^{2}}{{b}^{2}}$)恒成立,根据基本不等式的性质,求出即可.
解答 解:∵a,b,c为直角三角形的三边,其中c是斜边,
∴a2+b2=c2,
若$\frac{1}{{a}^{2}}$+$\frac{4}{{b}^{2}}$+$\frac{t}{{c}^{2}}$≥0恒成立,
则t≥-($\frac{{c}^{2}}{{a}^{2}}$+$\frac{{4c}^{2}}{{b}^{2}}$)
=-(1+$\frac{{b}^{2}}{{a}^{2}}$+4+$\frac{{4a}^{2}}{{b}^{2}}$)
=-(5+2$\sqrt{4}$)
=-9,
当且仅当a=b时“=”成立,
故答案为:[-9,+∞).
点评 本题考查了基本不等式的性质,考查勾股定理,是一道基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
10.在等比数列{an}中,a3,a9是方程3x2-11x+9=0的两个根,则a5a6a7=( )
| A. | 3$\sqrt{3}$ | B. | $\frac{11}{2}$ | C. | ±3$\sqrt{3}$ | D. | 以上皆非 |
4.已知x,y满足约束条件$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}≤4}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$,则z=3x+y的最大值为( )
| A. | 2$\sqrt{10}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 2$\sqrt{5}$ |
11.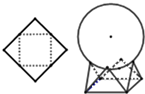 如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
 如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )
如图,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4}{3}$π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )| A. | $\frac{\sqrt{6}}{2}+\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{2}}}{2}+\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$+$\frac{3}{2}$ |
9.用反证法证明某命题时,对结论“a、b、c、d中至少有三个是正数”正确的反设是( )
| A. | a、b、c、d中至多有三个是正数 | B. | a、b、c、d中至多有两个是正数 | ||
| C. | a、b、c、d都是正数 | D. | a、b、c、d都是负数 |