题目内容
3．
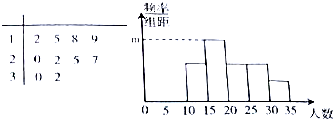从某校随机抽取10个班，调查各班中有网购经历的人数，所得数据的茎叶图和频率分布直方图如图所示．（分组区间依次为[10，15），[15，20），[20，25），[25，30），[30，35））（1）求所调查的班级中有网购经历的人数的中位数、平均数及频率分布直方图中m的值；
（2）若要从有网购物经历的人数在区间[20，30）内的班级中任取两个班，求其中至少有一个班有网购物经历的人数大于25的概率．
分析 （1）由茎叶图可知，中位数，求出平均数，第三组的频数为3，求出此组的频率，用频率÷组距得到m．
（2）由茎叶图可知，有网上购物经历的人数在区间[20，30]内的班级共有4个，通过列举法得到任取两个班级的方法数及至少有一个班有网上购物经历的方法数，利用古典概型的概率公式求出概率．
解答 解：（1）由茎叶图可知，中位数为21，
平均数为$\frac{1}{10}$（12+15+18+19+20+22+25+27+30+32）=22，
第二组的频数为3，频率为$\frac{3}{10}$=0.3，则m=$\frac{0.3}{5}$=0.06
（2）记事件Q：至少有一个班有网上购物经历的人数大于25．
由茎叶图可知，有网上购物经历的人数在区间[20，300]内的班级共有4个，不妨设为A，B，C，D，其中有网上购物经历的人数大于25的1个班级为A，
则从A，B，C，D中任取2个，有AB，AC，AD，BC，BD，CD，共6种，
其中满足题意的有AB，AC，AD，BE共3种
故P（Q）=$\frac{3}{6}$=0.5
点评 本题考查茎叶图及频率分布直方图，古典概型的概率公式，属于一道基础题
练习册系列答案
相关题目
13．正方形ABCD的边长为2，E是线段CD的中点，F是线段BE上的动点，则$\overrightarrow{BF}•\overrightarrow{FC}$的取值范围是（ ）
| A． | [1，0] | B． | $[-1，\frac{4}{5}]$ | C． | $[-\frac{4}{5}，1]$ | D． | [0，1] |
11．
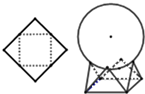如图，用一边长为$\sqrt{2}$的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为$\frac{4}{3}$π的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋最高点与蛋巢底面的距离为 （ ）
如图，用一边长为$\sqrt{2}$的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为$\frac{4}{3}$π的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋最高点与蛋巢底面的距离为 （ ）| A． | $\frac{\sqrt{6}}{2}+\frac{3}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{{\sqrt{2}}}{2}+\frac{3}{2}$ | D． | $\frac{\sqrt{3}}{2}$+$\frac{3}{2}$ |
