题目内容
20．已知随机变量X服从正态分布N（1，σ2），且P（X≤0）=0.1，则P（X＞2）=（ ）| A． | 0.9 | B． | 0.1 | C． | 0.6 | D． | 0.4 |
分析 随机变量ξ服从正态分布N（1，σ2），得到曲线关于x=1对称，根据曲线的对称性得到小于等于0的概率和大于等于2的概率是相等的得到结果．
解答 解：随机变量ξ服从正态分布N（1，σ2），
∴曲线关于x=1对称，
∴P（X＞2）=P（X≤0）=0.1
故选：B．
点评 本题主要考查正态分布曲线的特点及曲线所表示的意义、函数图象对称性的应用等基础知识，属于基础题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
10．在等比数列{an}中，a3，a9是方程3x2-11x+9=0的两个根，则a5a6a7=（ ）
| A． | 3$\sqrt{3}$ | B． | $\frac{11}{2}$ | C． | ±3$\sqrt{3}$ | D． | 以上皆非 |
11．
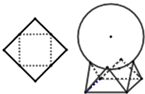如图，用一边长为$\sqrt{2}$的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为$\frac{4}{3}$π的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋最高点与蛋巢底面的距离为 （ ）
如图，用一边长为$\sqrt{2}$的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为$\frac{4}{3}$π的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋最高点与蛋巢底面的距离为 （ ）| A． | $\frac{\sqrt{6}}{2}+\frac{3}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{{\sqrt{2}}}{2}+\frac{3}{2}$ | D． | $\frac{\sqrt{3}}{2}$+$\frac{3}{2}$ |
9．用反证法证明某命题时，对结论“a、b、c、d中至少有三个是正数”正确的反设是（ ）
| A． | a、b、c、d中至多有三个是正数 | B． | a、b、c、d中至多有两个是正数 | ||
| C． | a、b、c、d都是正数 | D． | a、b、c、d都是负数 |