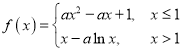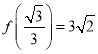题目内容
【题目】已知有穷数列![]() 共有
共有![]() 项
项![]() ,且
,且![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,试写出一个满足条件的数列
,试写出一个满足条件的数列![]() ;
;
(2)若![]() ,
,![]() ,求证:数列
,求证:数列![]() 为递增数列的充要条件是
为递增数列的充要条件是![]() ;
;
(3)若![]() ,则
,则![]() 所有可能的取值共有多少个?请说明理由.
所有可能的取值共有多少个?请说明理由.
【答案】(1)![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 或
或![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)有穷数列![]() 共有
共有![]() 项
项![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,由此能写出满足条件的数列
,由此能写出满足条件的数列![]() ;
;
(2)若数列![]() 为递增数列,由题意得
为递增数列,由题意得![]() ,
,![]() ,
,![]() ,
,![]() ,由此能推导出
,由此能推导出![]() ,由题意得
,由题意得![]() ,
,![]() ,
,![]() ,推导出
,推导出![]() ,
,![]() ,
,![]() ,
,![]() ,由
,由![]() ,推导出
,推导出![]() ,
,![]() ,
,![]() ,从而数列
,从而数列![]() 是递增数列,由此能证明数列
是递增数列,由此能证明数列![]() 为递增数列的充要条件为
为递增数列的充要条件为![]() ;
;
(3)由题意得![]() ,
,![]() ,
,![]() ,
,![]() ,推导出
,推导出![]() 的所有可能值与
的所有可能值与![]() 最大值的差必为偶数,用数学归纳法证明
最大值的差必为偶数,用数学归纳法证明![]() 可以取到
可以取到![]() 与
与![]() 之间相差
之间相差![]() 的所有整数,由此能求出
的所有整数,由此能求出![]() 所有可能取值的个数.
所有可能取值的个数.
(1)有穷数列![]() 共有
共有![]() 项
项![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则满足条件的数列![]() 有:
有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 或
或![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ;
;
(2)①充分性:若数列![]() 为递增数列,由题意得:
为递增数列,由题意得:![]() ,
,![]() ,
,![]() ,
,![]() ,全加得
,全加得![]() ,
,![]() ;
;
②必要性:由题意![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
上述不等式全部相加得![]() ,
,![]() ,
,
![]() ,所以,不等式
,所以,不等式![]() ,
,![]() ,
,![]() ,
,![]() 均取等号,
均取等号,
所以,![]() ,
,![]() ,
,![]() ,则数列
,则数列![]() 为单调递增数列.
为单调递增数列.
综上所述,数列![]() 为递增数列的充要条件是
为递增数列的充要条件是![]() ;
;
(3)由题意得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
假设![]() ,其中
,其中![]() ,
,
![]() ,
,
则![]() ,
,
则![]() 中有
中有![]() 项
项![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 取负值,
取负值,
则有![]() ,(*),
,(*),
![]() 的所有可能值与
的所有可能值与![]() 的差必为偶数,
的差必为偶数,
下面利用数学归纳法证明![]() 可以取到
可以取到![]() 与
与![]() 之间相差
之间相差![]() 的所有整数,
的所有整数,
由(*)知,还要从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中任取一项或若干项相加,可以得到从
中任取一项或若干项相加,可以得到从![]() 到
到![]() 的所有整数值即可.
的所有整数值即可.
①当![]() 时,显然成立;
时,显然成立;
②当![]() 时,从
时,从![]() 、
、![]() 中任取一项或两项相加,可以得到从
中任取一项或两项相加,可以得到从![]() 、
、![]() 、
、![]() 中任取一项或若干项相加,可以得到从
中任取一项或若干项相加,可以得到从![]() 到
到![]() 的所有整数,结论成立;
的所有整数,结论成立;
③假设当![]() 时,结论成立,即从
时,结论成立,即从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中任取一项或若干项相加,可以得到从
中任取一项或若干项相加,可以得到从![]() 到
到![]() 的所有整数值.
的所有整数值.
则当![]() 时,由假设,从
时,由假设,从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中任取一项或若干项相加,可以得到从
中任取一项或若干项相加,可以得到从![]() 到
到![]() 的所有整数值,
的所有整数值,
用![]() 取代
取代![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中的
中的![]() ,可得
,可得![]() ,
,
用![]() 取代
取代![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中的
中的![]() ,可得
,可得![]() ,
,
![]()
用![]() 取代
取代![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中的
中的![]() ,可得
,可得![]() ,
,
将![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 全部相加,可得
全部相加,可得![]() ,故命题成立.
,故命题成立.
因此,![]() 所有可能的取值共有
所有可能的取值共有 个.
个.

 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案【题目】某种零件的质量指标值为整数,指标值为8时称为合格品,指标值为7或者9时称为准合格品,指标值为6或10时称为废品,某单位拥有一台制造该零件的机器,为了了解机器性能,随机抽取了该机器制造的100个零件,不同的质量指标值对应的零件个数如下表所示;
质量指标值 | 6 | 7 | 8 | 9 | 10 |
零件个数 | 6 | 18 | 60 | 12 | 4 |
使用该机器制造的一个零件成本为5元,合格品可以以每个![]() 元的价格出售给批发商,准合格品与废品无法岀售.
元的价格出售给批发商,准合格品与废品无法岀售.
(1)估计该机器制造零件的质量指标值的平均数;
(2)若该单位接到一张订单,需要该零件2100个,为使此次交易获利达到1400元,估计![]() 的最小值;
的最小值;
(3)该单位引进了一台加工设备,每个零件花费2元可以被加工一次,加工结果会等可能出现以下三种情况:①质量指标值增加1,②质量指标值不变,③质量指标值减少1.已知每个零件最多可被加工一次,且该单位计划将所有准合格品逐一加工,在(2)的条件下,估计![]() 的最小值(精确到0.01) .
的最小值(精确到0.01) .