题目内容
【题目】正方体![]() 的棱长为2,动点
的棱长为2,动点![]() 在对角线
在对角线![]() 上,过点
上,过点![]() 作垂直于
作垂直于![]() 的平面
的平面![]() ,记平面
,记平面![]() 截正方体得到的截面多边形(含三角形)的周长为
截正方体得到的截面多边形(含三角形)的周长为![]() ,设
,设![]() .
.
(1)下列说法中,正确的编号为__________.
①截面多边形可能为四边形;②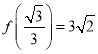 ;③函数
;③函数![]() 的图象关于
的图象关于![]() 对称.
对称.
(2)当![]() 时,三棱锥
时,三棱锥![]() 的外接球的表面积为__________.
的外接球的表面积为__________.
【答案】②③ 9π
【解析】
(1)先找到两个与![]() 垂直的平面作为辅助平面,从而确定这两个平面之间的截面为六边形,从而判断①错误;由正方体的对称性判断③;由等体积法判断②;
垂直的平面作为辅助平面,从而确定这两个平面之间的截面为六边形,从而判断①错误;由正方体的对称性判断③;由等体积法判断②;
(2)找出该三棱锥外接球的半径,由球的表面积公式计算即可.
(1)连接![]() ,
,![]() 以点D为坐标原点,分别以
以点D为坐标原点,分别以![]() 为
为![]() 轴建立如下图所示的空间直角坐标系
轴建立如下图所示的空间直角坐标系
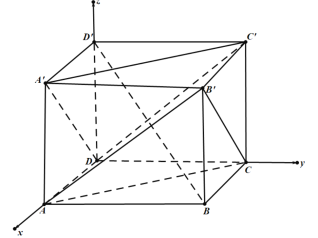
![]()
![]()
![]() ,
,![]()
所以![]() ,
,![]() 面
面![]() ,
,![]()
即![]() 面
面![]()
同理可证:![]() 面
面![]()
所以面![]() 面
面![]() ,如下图所示,夹在面
,如下图所示,夹在面![]() 和面
和面![]() 之间并且与这两个平面平行的截面为六边形
之间并且与这两个平面平行的截面为六边形
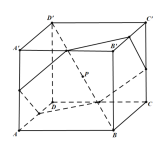
故截面只能为三角形和六边形,故①错误;
由正方体的对称性,可得函数![]() 的图像关于
的图像关于![]() 对称,故③正确;
对称,故③正确;
取 的中点分别为
的中点分别为![]() ,连接
,连接![]() ,如下图所示
,如下图所示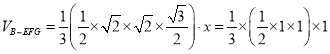 ,即此时
,即此时![]()
对应![]() 的周长为
的周长为![]() ,即
,即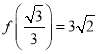 ,故②正确;
,故②正确;

(2)当![]() 时,此时点P在线段
时,此时点P在线段![]() 的中点,连接
的中点,连接![]() 交于点H
交于点H
则![]() ,
,![]() ,则
,则![]()
所以![]() ,同理可证:
,同理可证:![]()
![]() 面
面![]() ,
,![]() ,所以
,所以![]() 面
面![]()
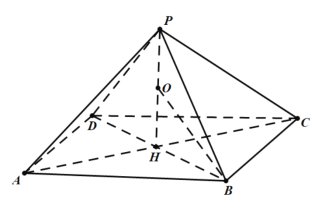
取PH的中点为O,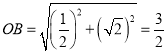 ,则三棱锥
,则三棱锥![]() 的外接球的球心为O,半径为
的外接球的球心为O,半径为![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]()
故答案为:(1)②③;(2)![]()

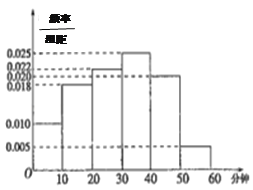
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成上面的2×2列联表,若按95%的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
(2)现在从该地区非体育迷的电视观众中,采用分层抽样方法选取5名观众,求从这5名观众选取两人进行访谈,被抽取的2名观众中至少有一名女生的概率.
附:![]()
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |