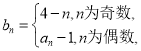题目内容
【题目】已知双曲线![]() 的左右顶点分别为
的左右顶点分别为![]() .直线
.直线![]() 和两条渐近线交于点
和两条渐近线交于点![]() ,点
,点![]() 在第一象限且
在第一象限且![]() ,
,![]() 是双曲线上的任意一点.
是双曲线上的任意一点.
(1)求双曲线的标准方程;
(2)是否存在点P使得![]() 为直角三角形?若存在,求出点P的个数;
为直角三角形?若存在,求出点P的个数;
(3)直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() ,证明:以
,证明:以![]() 为直径的圆必过定点.
为直径的圆必过定点.
【答案】(1) ![]() ;(2)4个;(3)证明过程见解析.
;(2)4个;(3)证明过程见解析.
【解析】
(1)根据![]() ,可知
,可知![]() ,根据题意求出点
,根据题意求出点![]() 的坐标,根据
的坐标,根据![]() ,求出
,求出![]() ,这样可求出双曲线的标准方程;
,这样可求出双曲线的标准方程;
(2)分类讨论以![]() 三点为直角顶点时能否构成直角三角形,最后确定点P的个数;
三点为直角顶点时能否构成直角三角形,最后确定点P的个数;
(3)设出点P的坐标,根据三点共线,结合斜率公式可以求出点![]() 的坐标,进而可求出以
的坐标,进而可求出以![]() 为直径的圆,最后根据圆的标准方程,可以判断出该圆所过的定点.
为直径的圆,最后根据圆的标准方程,可以判断出该圆所过的定点.
(1)因为![]() ,所以
,所以![]() ,双曲线的渐近线方程为:
,双曲线的渐近线方程为:![]() ,由题意可知:
,由题意可知:
![]() 而
而![]() ,所以
,所以![]() ,因此双曲线的标准方程为:
,因此双曲线的标准方程为:![]() ;
;
(2)因为直线![]() 的斜率为
的斜率为![]() ,所以与直线
,所以与直线![]() 垂直的直线的斜率为
垂直的直线的斜率为![]() ,设
,设![]() 点的坐标为:
点的坐标为:![]() ,则有
,则有![]() .
.
当![]() 时,所以
时,所以![]() 且
且![]() ,解得
,解得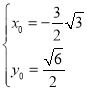 或
或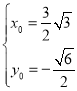 此时存在2个
此时存在2个![]() 点;
点;
当![]() 时,所以
时,所以![]() 且
且![]() ,
,![]() ,解得
,解得![]() 或
或![]() ,此时存在2个
,此时存在2个![]() 点;
点;
当![]() 时,此时
时,此时![]() 点是以线段
点是以线段![]() 为直径圆上,圆的方程为:
为直径圆上,圆的方程为: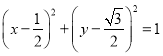 ,与双曲线方程联立,无实数解,
,与双曲线方程联立,无实数解,
综上所述:点P的个数为4个;
(3)设![]() 点的坐标为
点的坐标为![]() ,
,![]() .
.
因为![]() 三点共线,所以直线
三点共线,所以直线![]() 的斜率相等,即
的斜率相等,即 ![]()
![]()
因为![]() 三点共线,所以直线
三点共线,所以直线![]() 的斜率相等,即
的斜率相等,即 ![]() , 所以
, 所以![]() 的中点坐标为:
的中点坐标为:![]()
![]() ,所以以
,所以以![]() 为直径的圆的方程为:
为直径的圆的方程为:![]() ,即
,即![]()
令![]() 或
或![]() ,因此该圆恒过
,因此该圆恒过![]() 两点.
两点.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目