题目内容
【题目】已知离心率为![]() 的椭圆
的椭圆![]()
![]() 的左顶点为A,且椭圆E经过
的左顶点为A,且椭圆E经过![]() 与坐标轴不垂直的直线l与椭圆E交于C,D两点,且直线AC和直线AD的斜率之积为
与坐标轴不垂直的直线l与椭圆E交于C,D两点,且直线AC和直线AD的斜率之积为![]() .
.
(I)求椭圆E的标准方程;
(Ⅱ)求证:直线l过定点.
【答案】(I)![]() ;(II)证明见解析.
;(II)证明见解析.
【解析】
(Ⅰ)根据离心率,可得![]() 的关系,代入解析式,代入
的关系,代入解析式,代入![]() 的坐标,即可求得
的坐标,即可求得![]() ,进而得椭圆的标准方程.
,进而得椭圆的标准方程.
(Ⅱ)设出直线![]() 的方程
的方程![]() ,将直线方程与椭圆方程联立,根据有两个不同的交点可知
,将直线方程与椭圆方程联立,根据有两个不同的交点可知![]() ,利用韦达定理表示出
,利用韦达定理表示出![]() ,由直线AC和直线AD的斜率之积为
,由直线AC和直线AD的斜率之积为![]() 可得关于
可得关于![]() 和
和![]() 的方程,即可求得
的方程,即可求得![]() 和
和![]() 的关系,代入直线方程即可求得所过定点的坐标;也可将方程设为
的关系,代入直线方程即可求得所过定点的坐标;也可将方程设为![]() ,将直线方程与椭圆方程联立,根据有两个不同的交点可知
,将直线方程与椭圆方程联立,根据有两个不同的交点可知![]() ,利用韦达定理表示出
,利用韦达定理表示出![]() ,由直线AC和直线AD的斜率之积为
,由直线AC和直线AD的斜率之积为![]() 可得关于
可得关于![]() 和
和![]() 的方程,化简求得
的方程,化简求得![]() 的值,即可求得所过定点的坐标.
的值,即可求得所过定点的坐标.
(I)![]()
![]()
![]()
![]()
又![]() 椭圆E经过点
椭圆E经过点![]()
![]()
![]() 椭圆E的标准方程为
椭圆E的标准方程为![]()
(II)方法一:![]() 的方程为
的方程为![]() ,
,
设![]() ,
,
联立方程组 ,
,
化简得![]() ,
,
由![]() 解得
解得![]() ,
,
且![]()
![]() .
.
![]()
![]()
![]() ,
,
![]() ,
,
![]()
化简可得:![]()
![]() 或
或![]() (舍),满足
(舍),满足![]()
![]() 直线l的方程为
直线l的方程为![]() ,
,
![]() 直线l经过定点
直线l经过定点![]()
方法二:设l的方程为![]() ,
,
设![]()
![]() ,
,
联立方程组 ,
,
化简得![]() ,
,
![]() 解得:
解得:![]() ,
,
且![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]()
化简可得:![]()
![]() 或者
或者![]() (舍)满足
(舍)满足![]()
![]() 直线l经过定点
直线l经过定点![]() .
.

练习册系列答案
相关题目
【题目】高三学生为了迎接高考,要经常进行模拟考试,锻炼应试能力,某学生从升入高三到高考要参加10次模拟考试,下面是高三第一学期某学生参加5次模拟考试的数学成绩表:
模拟考试第x次 | 1 | 2 | 3 | 4 | 5 |
考试成绩y分 | 90 | 100 | 105 | 105 | 100 |
(1)已知该考生的模拟考试成绩y与模拟考试的次数x满足回归直线方程![]() ,若高考看作第11次模拟考试,试估计该考生的高考数学成绩;
,若高考看作第11次模拟考试,试估计该考生的高考数学成绩;
(2)把这5次模拟考试的数学成绩单放在5个相同的信封中,从中随机抽取3份试卷的成绩单进行研究,设抽取考试成绩不等于平均值![]() 的个数为
的个数为![]() ,求出
,求出![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式:
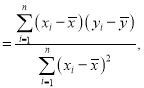
![]() .
.

