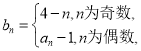题目内容
【题目】某种零件的质量指标值为整数，指标值为8时称为合格品，指标值为7或者9时称为准合格品，指标值为6或10时称为废品，某单位拥有一台制造该零件的机器，为了了解机器性能，随机抽取了该机器制造的100个零件，不同的质量指标值对应的零件个数如下表所示；
质量指标值 | 6 | 7 | 8 | 9 | 10 |
零件个数 | 6 | 18 | 60 | 12 | 4 |
使用该机器制造的一个零件成本为5元，合格品可以以每个
元的价格出售给批发商，准合格品与废品无法岀售.
（1）估计该机器制造零件的质量指标值的平均数；
（2）若该单位接到一张订单，需要该零件2100个，为使此次交易获利达到1400元，估计的最小值；
（3）该单位引进了一台加工设备，每个零件花费2元可以被加工一次，加工结果会等可能出现以下三种情况：①质量指标值增加1，②质量指标值不变，③质量指标值减少1.已知每个零件最多可被加工一次，且该单位计划将所有准合格品逐一加工，在（2）的条件下，估计的最小值（精确到0.01） .
【答案】（1）7.9个 （2）9 （3）8.67
【解析】
(1)用样本的平均值估计总体的平均数，即求出100个样本的平均数即可.
(2) 一个零件成本为5元，
的价格出售，可得式子：
可解出答案.
(3) 设为满足该订单需制作
个零件，则有
,求出需要制作的零件总数，然后再计算满足利润条件的值.
解：（1）设机器制造零件的质量指标值的平均数为
；
由题意得：
，
∴机器制造零件的质量指标值的平均数为7.9个.
（2）一个零件成本为5元，的价格出售，可得式子：
，
解得：
，
∴的最小值为9；
（3）依题意得，准合格品加工后有
能合格，用于销售，
设为满足该订单需制作个零件，则有
，
解得
，
故要使获利达到1400元，需要
，
解得
，
∴的最小值为8.67.
练习册系列答案
相关题目
