题目内容
2.已知数列{an}满足a1=-1,an=1-$\frac{1}{{{a_{n-1}}}}$(n>1),则a2015=( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
分析 由a1=-1,an=1-$\frac{1}{{{a_{n-1}}}}$(n>1),可得an+3=an.利用周期性即可得出.
解答 解:∵a1=-1,an=1-$\frac{1}{{{a_{n-1}}}}$(n>1),
∴a2=1-(-1)=2,a3=1-$\frac{1}{2}$=$\frac{1}{2}$,a4=1-2=-1,…,
∴an+3=an.
∴数列{an}是周期数列,周期T=3.
∴a2015=a3×671+2=a2=2.
故选:A.
点评 本题考查了递推式的应用、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
20.已知函数f(x)=2sin$\frac{x}{2}$的定义域为[a,b],值域为[-1,2],则b-a的值不可能是( )
| A. | $\frac{4π}{3}$ | B. | 2π | C. | $\frac{8π}{3}$ | D. | $\frac{14π}{3}$ |
17.在△ABC中,三边a,b,c满足a2=b2+c2+bc,则角A等于( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
14.若坐标原点到抛物线x2=$\frac{1}{m}$y的准线距离为2,则m=( )
| A. | $\frac{1}{8}$ | B. | ±$\frac{1}{8}$ | C. | 8 | D. | ±8 |
12.设条件p:a≥0;条件q:a2+a≥0,那么p是q的( )
| A. | 必要而不充分条件 | B. | 充分而不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
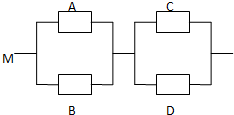 如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.
如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.