题目内容
11．
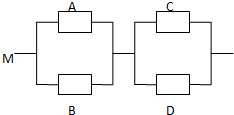如图，用A、B、C、D表示四类不同的元件连接成系统M．当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时，系统M正常工作．已知元件A、B、C、D正常工作的概率依次为：0.3、0.6、0.5、0.8，元件连接成的系统M正常工作的概率P（M）=0.648．
分析 根据对立事件概率间的关系，分别求出前一个系统AB正常的概率、后一个系统CD正常的概率，再相乘，即得所求．
解答 解：前一个系统AB正常的概率为1-0.7×0.4=0.72，后一个系统CD正常的概率为1-0.5×0.2=0.9，
故这2个系统都正常的概率为 0.72×0.9=0.648，
故答案为：0.648．
点评 本题主要考查相互独立事件的概率乘法公式，所求的事件的概率与它的对立事件的概率之间的关系，属于基础题．
练习册系列答案
相关题目
1．“x=0”是“（2x-1）x=0”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
2．已知数列{an}满足a1=-1，an=1-$\frac{1}{{{a_{n-1}}}}$（n＞1），则a2015=（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | -1 |
6．双曲线y=$\frac{1}{x}$在点（2，$\frac{1}{2}$）的切线方程是（ ）
| A． | $\frac{1}{4}$x+y=0 | B． | $\frac{1}{4}$x-y=0 | C． | $\frac{1}{4}$x+y+1=0 | D． | $\frac{1}{4}$x+y-1=0 |
20．已知|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=3，|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{19}$，则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于（ ）
| A． | $\sqrt{13}$ | B． | $\sqrt{15}$ | C． | $\sqrt{17}$ | D． | $\sqrt{7}$ |