题目内容
函数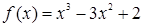 在区间
在区间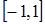 上的最大值是( )
上的最大值是( )
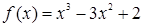 在区间
在区间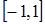 上的最大值是( )
上的最大值是( )A.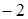 | B.0 | C.2 | D.4 |
C
试题分析:
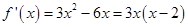 ,因为
,因为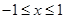 ,所以令
,所以令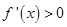 得
得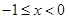 ,令
,令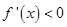 得
得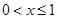 。所以函数
。所以函数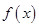 在
在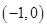 上单调递增,在
上单调递增,在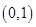 上单调递减。所以
上单调递减。所以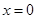 时函数
时函数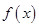 取得极大值同时也是最大值即
取得极大值同时也是最大值即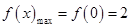 。故C正确。
。故C正确。
练习册系列答案
相关题目
题目内容
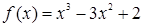 在区间
在区间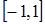 上的最大值是( )
上的最大值是( )A.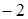 | B.0 | C.2 | D.4 |
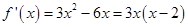 ,因为
,因为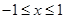 ,所以令
,所以令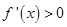 得
得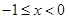 ,令
,令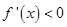 得
得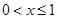 。所以函数
。所以函数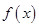 在
在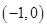 上单调递增,在
上单调递增,在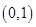 上单调递减。所以
上单调递减。所以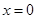 时函数
时函数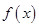 取得极大值同时也是最大值即
取得极大值同时也是最大值即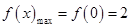 。故C正确。
。故C正确。