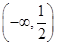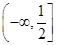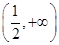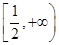题目内容
已知定义在R上的函数f(x)=-2x3+bx2+cx(b,c∈R),函数F(x)=f(x)-3x2是奇函数,函数f(x)满足 .
.
(1)求f(x)的解析式;
(2)讨论f(x)在区间(-3,3)上的单调性.
 .
.(1)求f(x)的解析式;
(2)讨论f(x)在区间(-3,3)上的单调性.
(1)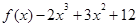 ;(2)单调递增区间为
;(2)单调递增区间为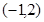 ,单调递减区间为
,单调递减区间为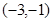 ,
,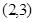 .
.
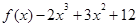 ;(2)单调递增区间为
;(2)单调递增区间为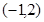 ,单调递减区间为
,单调递减区间为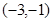 ,
,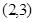 .
.试题分析:(1)先对
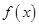 求导可得
求导可得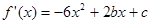 ,由
,由 得
得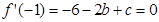 ,又F(x)=f(x)-3x2是奇函数,得
,又F(x)=f(x)-3x2是奇函数,得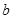 的值,代加上式可得
的值,代加上式可得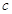 ,可得函数解析式;(2)由(1)知函数的导函数
,可得函数解析式;(2)由(1)知函数的导函数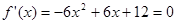 ,令
,令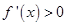 得增区间,令
得增区间,令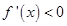 得减区间.
得减区间.试题解析:
解:(1)
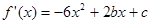 1分
1分F(x)=f(x)-3x2是奇函数,得
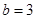 3分
3分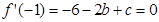 ,得
,得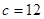 5分
5分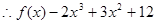 6分
6分(2)令
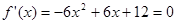 得
得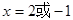 10分
10分 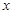 | 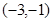 | 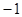 | 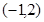 | 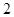 | 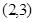 |
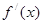 | - | 0 | + | 0 | - |
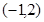
单调递减区间为
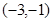 ,
,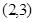 12分
12分
练习册系列答案
相关题目

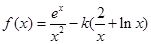 (
(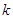 为常数,
为常数,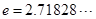 是自然对数的底数).
是自然对数的底数).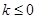 时,求函数
时,求函数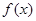 的单调区间;
的单调区间;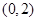 内存在两个极值点,求
内存在两个极值点,求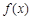 ,若对任意
,若对任意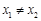 ,都有
,都有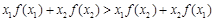 ,则称f(x)为“H函数”,给出下列函数:①
,则称f(x)为“H函数”,给出下列函数:①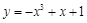 ;②
;② ;③
;③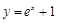 ;④
;④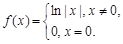 其中是“H函数”的个数为
其中是“H函数”的个数为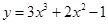 在区间
在区间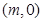 上为减函数, 则
上为减函数, 则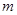 的取值范围是__ ___.
的取值范围是__ ___. 内不是增函数的是( )
内不是增函数的是( )



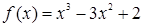 在区间
在区间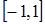 上的最大值是( )
上的最大值是( )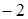
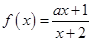 在
在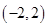 内为增函数,则实数
内为增函数,则实数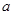 的取值范围是( )
的取值范围是( )