题目内容
已知函数f(x)=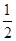 x2-alnx(a∈R).
x2-alnx(a∈R).
(1)若函数f(x)的图象在x=2处的切线方程为y=x+b,求a,b的值;
(2)若函数f(x)在(1,+∞)上为增函数,求a的取值范围.
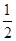 x2-alnx(a∈R).
x2-alnx(a∈R).(1)若函数f(x)的图象在x=2处的切线方程为y=x+b,求a,b的值;
(2)若函数f(x)在(1,+∞)上为增函数,求a的取值范围.
(1)a=2,b=-2ln2
(2)(-∞,1]
(2)(-∞,1]
解:(1)因为f′(x)=x-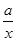 (x>0),
(x>0),
又f(x)在x=2处的切线方程为y=x+b,斜率为1,
所以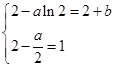
解得a=2,b=-2ln2.
(2)若函数f(x)在(1,+∞)上为增函数,
则f′(x)=x-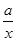 ≥0在(1,+∞)上恒成立,
≥0在(1,+∞)上恒成立,
即a≤x2在(1,+∞)上恒成立.
所以a≤1.检验当a=1时满足题意.
故a的取值范围是(-∞,1].
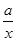 (x>0),
(x>0),又f(x)在x=2处的切线方程为y=x+b,斜率为1,
所以
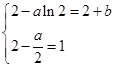
解得a=2,b=-2ln2.
(2)若函数f(x)在(1,+∞)上为增函数,
则f′(x)=x-
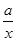 ≥0在(1,+∞)上恒成立,
≥0在(1,+∞)上恒成立,即a≤x2在(1,+∞)上恒成立.
所以a≤1.检验当a=1时满足题意.
故a的取值范围是(-∞,1].

练习册系列答案
相关题目

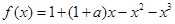 ,其中
,其中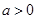
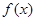 在其定义域上的单调性;
在其定义域上的单调性;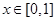 时,求
时,求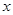 的值.
的值.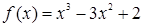 在区间
在区间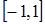 上的最大值是( )
上的最大值是( )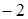
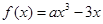 .
.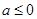 时,求函数
时,求函数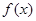 单调区间;
单调区间;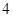 ,求
,求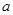 的值.
的值.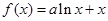 ,对任意的
,对任意的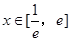 时,
时,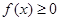 恒成立,则a的范围为 .
恒成立,则a的范围为 .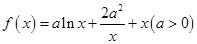 .若曲线
.若曲线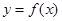 在点
在点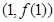 处的切线与直线
处的切线与直线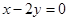 垂直,
垂直,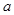 的值;
的值;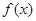 的单调区间;
的单调区间;