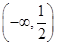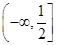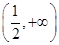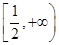题目内容
设函数f(x)=ln x-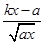 -ln a(x>0,a>0且为常数).
-ln a(x>0,a>0且为常数).
(1)当k=1时,判断函数f(x)的单调性,并加以证明;
(2)当k=0时,求证:f(x)>0对一切x>0恒成立;
(3)若k<0,且k为常数,求证:f(x)的极小值是一个与a无关的常数.
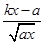 -ln a(x>0,a>0且为常数).
-ln a(x>0,a>0且为常数).(1)当k=1时,判断函数f(x)的单调性,并加以证明;
(2)当k=0时,求证:f(x)>0对一切x>0恒成立;
(3)若k<0,且k为常数,求证:f(x)的极小值是一个与a无关的常数.
(1)见解析 (2)见解析 (3)见解析
解:(1)当k=1时,
f(x)=ln x-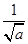 ·x
·x +
+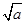 x-
x- -ln a,
-ln a,
因为f′(x)=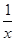 -
-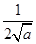 ·x-
·x- -
-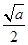 x-
x-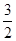
=-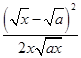 ≤0,
≤0,
所以函数f(x)在(0,+∞)上是单调减函数.
(2)证明:当k=0时,
f(x)=ln x+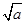 x-
x- -ln a,故
-ln a,故
f′(x)=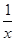 -
-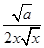 =
=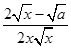 .
.
令f′(x)=0,解得x=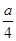 .
.
当0<x<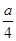 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在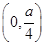 上是单调减函数;
上是单调减函数;
当x>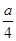 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在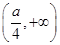 上是单调增函数.
上是单调增函数.
所以当x=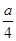 时,f′(x)有极小值,
时,f′(x)有极小值,
为f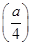 =2-2ln 2.
=2-2ln 2.
因为e>2,所以f(x)的极小值,
为f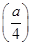 =2(1-ln 2)=2ln
=2(1-ln 2)=2ln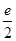 >0.
>0.
所以当k=0时,f(x)>0对一切x>0恒成立.
(3)证明:
f(x)=ln x- ·x
·x +
+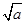 x-
x- -ln a,
-ln a,
所以f′(x)=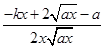 .
.
令f′(x0)=0,得kx0-2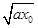 +a=0.
+a=0.
所以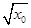 =
=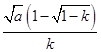
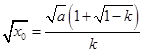 (舍去).
(舍去).
所以x0=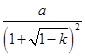 .
.
当0<x<x0时,f′(x)<0,f(x)在(0,x0)上是单调减函数;
当x>x0时,f′(x)>0,f(x)在(x0,+∞)上是单调增函数.
因此,当x=x0时,f(x)有极小值f(x0).
又f(x0)=ln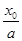 -k
-k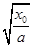 +
+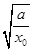 ,
,
而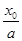 =
=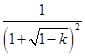 是与a无关的常数,所以ln
是与a无关的常数,所以ln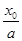 ,-k
,-k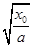 ,
,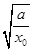 均与a无关.
均与a无关.
所以f(x0)是与a无关的常数.
故f(x)的极小值是一个与a无关的常数.
f(x)=ln x-
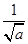 ·x
·x +
+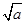 x-
x- -ln a,
-ln a,因为f′(x)=
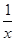 -
-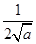 ·x-
·x- -
-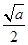 x-
x-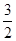
=-
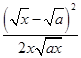 ≤0,
≤0,所以函数f(x)在(0,+∞)上是单调减函数.
(2)证明:当k=0时,
f(x)=ln x+
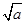 x-
x- -ln a,故
-ln a,故f′(x)=
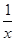 -
-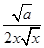 =
=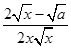 .
.令f′(x)=0,解得x=
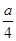 .
.当0<x<
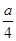 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在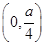 上是单调减函数;
上是单调减函数;当x>
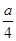 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在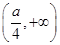 上是单调增函数.
上是单调增函数.所以当x=
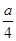 时,f′(x)有极小值,
时,f′(x)有极小值,为f
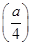 =2-2ln 2.
=2-2ln 2.因为e>2,所以f(x)的极小值,
为f
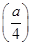 =2(1-ln 2)=2ln
=2(1-ln 2)=2ln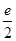 >0.
>0.所以当k=0时,f(x)>0对一切x>0恒成立.
(3)证明:
f(x)=ln x-
 ·x
·x +
+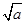 x-
x- -ln a,
-ln a,所以f′(x)=
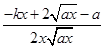 .
.令f′(x0)=0,得kx0-2
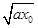 +a=0.
+a=0.所以
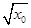 =
=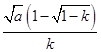
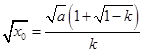 (舍去).
(舍去).所以x0=
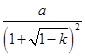 .
.当0<x<x0时,f′(x)<0,f(x)在(0,x0)上是单调减函数;
当x>x0时,f′(x)>0,f(x)在(x0,+∞)上是单调增函数.
因此,当x=x0时,f(x)有极小值f(x0).
又f(x0)=ln
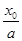 -k
-k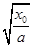 +
+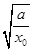 ,
,而
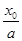 =
=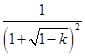 是与a无关的常数,所以ln
是与a无关的常数,所以ln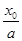 ,-k
,-k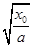 ,
,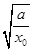 均与a无关.
均与a无关.所以f(x0)是与a无关的常数.
故f(x)的极小值是一个与a无关的常数.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
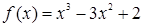 在区间
在区间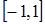 上的最大值是( )
上的最大值是( )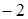
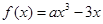 .
.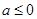 时,求函数
时,求函数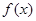 单调区间;
单调区间;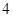 ,求
,求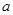 的值.
的值.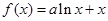 ,对任意的
,对任意的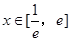 时,
时,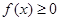 恒成立,则a的范围为 .
恒成立,则a的范围为 .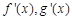 分别是二次函数
分别是二次函数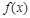 和三次函数
和三次函数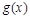 的导函数,它们在同一坐标系内的图象如图所示.
的导函数,它们在同一坐标系内的图象如图所示.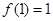 ,则
,则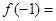 ;
;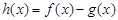 ,则
,则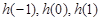 的大小关系为 (用“<”连接).
的大小关系为 (用“<”连接).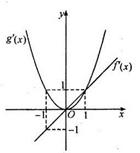
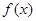 满足
满足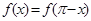 且当
且当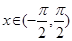 时,
时,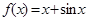 ,则( )
,则( )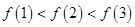
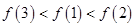
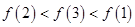
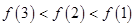
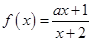 在
在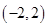 内为增函数,则实数
内为增函数,则实数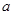 的取值范围是( )
的取值范围是( )