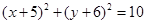题目内容
两圆相交于两点 和
和 ,两圆圆心都在直线
,两圆圆心都在直线 上,且
上,且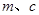 均为实数,则
均为实数,则 .
.
 和
和 ,两圆圆心都在直线
,两圆圆心都在直线 上,且
上,且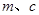 均为实数,则
均为实数,则 .
. 3
试题分析:根据题意,由相交弦的性质,相交两圆的连心线垂直平分相交弦,
可得AB与直线
 垂直,且AB的中点在这条直线
垂直,且AB的中点在这条直线 上;
上;由AB与直线
 垂直,可得
垂直,可得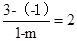
解可得m=-1,则B(-1,-1),
故AB中点为(0,1),且其在直线
 .代入直线方程可得,0-1×(1)+c=0,可得c=4;故m+c=(-1)+(4)=3;故选A.
.代入直线方程可得,0-1×(1)+c=0,可得c=4;故m+c=(-1)+(4)=3;故选A.点评:本题考查相交弦的性质,解题的关键在于利用相交弦的性质,即两圆的连心线垂直平分相交弦.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与直线
与直线 及
及 都相切,且圆心在直线
都相切,且圆心在直线 上,则圆
上,则圆 :
: ,过
,过 轴上的点
轴上的点 存在圆
存在圆 ,使得
,使得 ,则点
,则点 的横坐标
的横坐标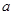 的取值范围是( )
的取值范围是( )



 的方程为:
的方程为: .
. 的值,使圆
的值,使圆 的直线方程.
的直线方程. 为圆
为圆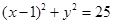 的弦AB的中点, 则直线AB的方程为 。
的弦AB的中点, 则直线AB的方程为 。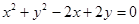 的周长是( )
的周长是( )



 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与

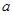 ,
,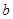 ,
,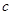 成等差数列且公差不为零,则直线
成等差数列且公差不为零,则直线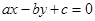 被圆
被圆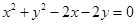 截得的弦长的最小值为_______.
截得的弦长的最小值为_______.