题目内容
已知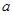 ,
,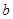 ,
,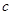 成等差数列且公差不为零,则直线
成等差数列且公差不为零,则直线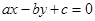 被圆
被圆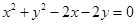 截得的弦长的最小值为_______.
截得的弦长的最小值为_______.
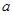 ,
,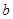 ,
,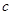 成等差数列且公差不为零,则直线
成等差数列且公差不为零,则直线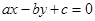 被圆
被圆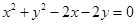 截得的弦长的最小值为_______.
截得的弦长的最小值为_______.2;
试题分析:
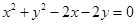 的圆心为C(1,1),半径为
的圆心为C(1,1),半径为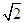 。
。因为a,b,c是等差数列,所以有a-2b+c=0,由ax-by+c=0,知直线过定点A(1,2),所以直线
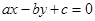 被圆
被圆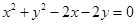 截得的弦长的最小值,应是在AC垂直于直线
截得的弦长的最小值,应是在AC垂直于直线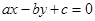 是取到,在弦的一半、半径、圆心到直线的距离构成的直角三角形中,由勾股定理得弦长为2。
是取到,在弦的一半、半径、圆心到直线的距离构成的直角三角形中,由勾股定理得弦长为2。点评:中档题,涉及正弦被圆截得弦长问题,往往借助于弦的一半、半径、圆心到直线的距离构成的直角三角形。

练习册系列答案
相关题目
 的方程为
的方程为 ,直线
,直线 过点
过点 ,且与圆
,且与圆 轴交于
轴交于 两点,
两点, 是圆
是圆 且与
且与 ,直线
,直线 交直线
交直线 ,直线
,直线 交直线
交直线 .求证:
.求证: 的外接圆总过定点,并求出定点坐标.
的外接圆总过定点,并求出定点坐标. 的最小值为 .
的最小值为 . 和
和 ,两圆圆心都在直线
,两圆圆心都在直线 上,且
上,且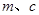 均为实数,则
均为实数,则 .
.  的边
的边 所在直线的方程为
所在直线的方程为 ,
, 满足
满足 , 点
, 点 在
在 所在直线上且
所在直线上且 .
. 
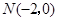 ,且与
,且与 的方程;
的方程; 斜率为
斜率为 的直线与曲线
的直线与曲线 两点,满足
两点,满足 ,求
,求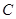 和
和 轴相切,圆心在直线
轴相切,圆心在直线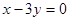 上,且被直线
上,且被直线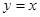 截得的弦长为
截得的弦长为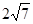
 ,求圆
,求圆 关于
关于 对称的圆的方程是( )
对称的圆的方程是( )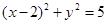



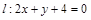 及圆
及圆 的交点,并且有最小面积的圆
的交点,并且有最小面积的圆 的方程为
的方程为  平分的直线是( )
平分的直线是( )


