题目内容
若 为圆
为圆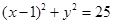 的弦AB的中点, 则直线AB的方程为 。
的弦AB的中点, 则直线AB的方程为 。
 为圆
为圆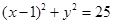 的弦AB的中点, 则直线AB的方程为 。
的弦AB的中点, 则直线AB的方程为 。
试题分析:根据题意可知,由于
 为圆
为圆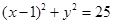 的弦AB的中点,因此圆心(1,0),半径为5,可知点P在直线AB上,其斜率为
的弦AB的中点,因此圆心(1,0),半径为5,可知点P在直线AB上,其斜率为 的两点斜率的负倒数,即可知为1,因此由点斜式方程可知为
的两点斜率的负倒数,即可知为1,因此由点斜式方程可知为 ,答案为
,答案为 。
。点评:根据直线与圆的位置关系可知,圆内弦所在直线与圆心和弦中点的连线垂直,这是解题的关键。基础题

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
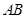 是
是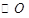 的直径,
的直径,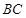 是
是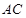 与
与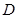 ,若
,若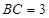 ,
,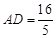 ,则
,则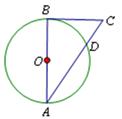
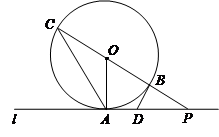
 (1)判断直线DB与⊙O的位置关系,并说明理由;
(1)判断直线DB与⊙O的位置关系,并说明理由;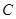 :
: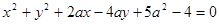 上所有的点均在第二象限内,则
上所有的点均在第二象限内,则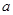 的取值范围为 。
的取值范围为 。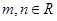 ,若直线
,若直线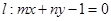 与
与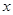 轴相交于点
轴相交于点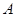 ,与
,与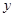 轴相交于
轴相交于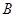 ,且
,且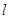 与圆
与圆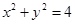 相交所得弦的长为2,
相交所得弦的长为2,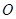 为坐标原点,求
为坐标原点,求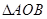 面积的最小值.
面积的最小值. 和
和 ,两圆圆心都在直线
,两圆圆心都在直线 上,且
上,且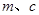 均为实数,则
均为实数,则 .
. 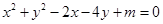 .
.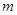 的取值范围;
的取值范围;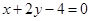 相交于
相交于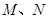 两点,且
两点,且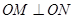 (
(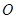 为坐标原点)求
为坐标原点)求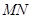 为直径的圆的方程.
为直径的圆的方程. 的边
的边 所在直线的方程为
所在直线的方程为 ,
, 满足
满足 , 点
, 点 在
在 所在直线上且
所在直线上且 .
. 
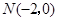 ,且与
,且与 的方程;
的方程; 斜率为
斜率为 的直线与曲线
的直线与曲线 两点,满足
两点,满足 ,求
,求 轴上,且过两点A(1,4),B(3,2)的圆的方程为 .
轴上,且过两点A(1,4),B(3,2)的圆的方程为 .