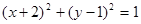题目内容
(本小题满分10分)选修4-1几何证明选讲
如图,AB是 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 o 上不同于A、B的一点,AD为
o 上不同于A、B的一点,AD为 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与 O交于D,与BE交于E,连结BD、CD.
O交于D,与BE交于E,连结BD、CD.

(I )求证:BD平分
(II)求证:AH.BH=AE.HC
如图,AB是
 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 o 上不同于A、B的一点,AD为
o 上不同于A、B的一点,AD为 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与 O交于D,与BE交于E,连结BD、CD.
O交于D,与BE交于E,连结BD、CD.
(I )求证:BD平分

(II)求证:AH.BH=AE.HC
(1)结合弦切角定理来证明角相等,从而得到平分问题。
(2)利用三角形的相似来得到对应线段的长度之积相等。
(2)利用三角形的相似来得到对应线段的长度之积相等。
试题分析:证明:(Ⅰ)由弦切角定理知
 …………2分
…………2分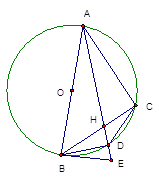
由
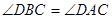 ,
,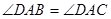
所以
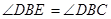 , 即
, 即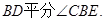 …………5分
…………5分(Ⅱ)由(Ⅰ)可知
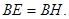
所以
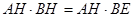 ,……………7分
,……………7分因为
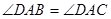 ,
,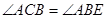 ,
,所以
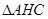 ∽
∽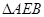 ,
,所以
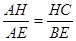 ,即
,即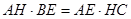 …………10分
…………10分即:
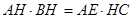 .
.点评:解决该试题的关键是对于平分角的求解,可以利用角相等,结合弦切角定理来得到角相等的证明,同时利用相似三角形来证明对应边的乘积相等,培养分析问题和解决问题的能力,属于中档题。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 的方程为
的方程为 ,直线
,直线 过点
过点 ,且与圆
,且与圆 轴交于
轴交于 两点,
两点, 是圆
是圆 且与
且与 ,直线
,直线 交直线
交直线 ,直线
,直线 交直线
交直线 .求证:
.求证: 的外接圆总过定点,并求出定点坐标.
的外接圆总过定点,并求出定点坐标. 是圆
是圆 的直径,
的直径, 是弦,
是弦, ,垂足为
,垂足为 ,
, 。
。
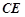 与圆
与圆 。
。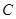 :
: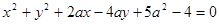 上所有的点均在第二象限内,则
上所有的点均在第二象限内,则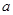 的取值范围为 。
的取值范围为 。 和
和 ,两圆圆心都在直线
,两圆圆心都在直线 上,且
上,且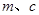 均为实数,则
均为实数,则 .
. 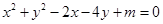 .
.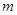 的取值范围;
的取值范围;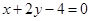 相交于
相交于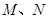 两点,且
两点,且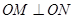 (
(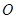 为坐标原点)求
为坐标原点)求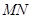 为直径的圆的方程.
为直径的圆的方程. 的边
的边 所在直线的方程为
所在直线的方程为 ,
, 满足
满足 , 点
, 点 在
在 所在直线上且
所在直线上且 .
. 
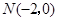 ,且与
,且与 的方程;
的方程; 斜率为
斜率为 的直线与曲线
的直线与曲线 两点,满足
两点,满足 ,求
,求 关于
关于 对称的圆的方程是( )
对称的圆的方程是( )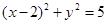



 与圆
与圆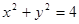 上任一点连线的中点轨迹方程是( )
上任一点连线的中点轨迹方程是( )