题目内容
(本题满分12分)
已知函数 满足
满足 .
.
(1)求常数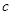 的值;
的值;
(2)求使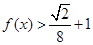 成立的x的取值范围.
成立的x的取值范围.
已知函数
 满足
满足 .
.(1)求常数
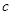 的值;
的值; (2)求使
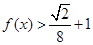 成立的x的取值范围.
成立的x的取值范围.(1)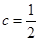 .(2)
.(2)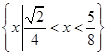 .
.
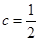 .(2)
.(2)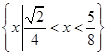 .
. 试题分析:(1)根据已知条件分析函数的定义域的范围,进而得到一个结论,那就是由于
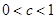 ,所以
,所以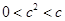 ,进而解决了第一问,。
,进而解决了第一问,。(2)在第一问的基础上那么
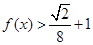 的解集也就分类讨论得到。
的解集也就分类讨论得到。解:(1)因为
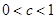 ,所以
,所以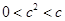 ;由
;由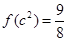 ,即
,即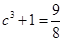 ,
,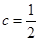 .(4分)
.(4分)(2)
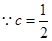 ,
,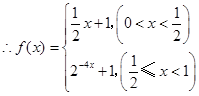 (6分)
(6分)当
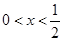 时,由
时,由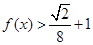 得
得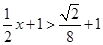 ,从而
,从而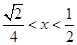 ,(8分)
,(8分)当
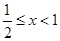 时,解
时,解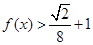 得
得 ,从而
,从而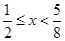 ,(10分)
,(10分)综上可得,
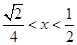 或
或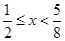 ,即
,即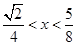 (11分)
(11分)所以
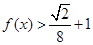 的解集为
的解集为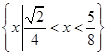 .(12分)
.(12分)点评:解决该试题的关键是能利用函数中由于
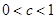 ,所以
,所以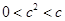 ;由
;由 ,即得到参数c的值。分析这一点是个难点,也是突破口。
,即得到参数c的值。分析这一点是个难点,也是突破口。
练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
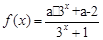 .
. 
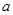 使函数f(x)为奇函数?证明你的结论;
使函数f(x)为奇函数?证明你的结论;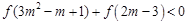 .
. 是偶函数,
是偶函数,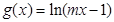 在
在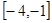 内单调递减,则实数
内单调递减,则实数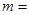 。
。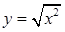 与
与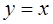
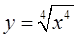 与
与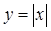
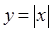 与
与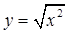 与
与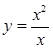
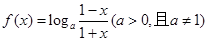
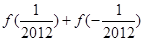 的值;
的值;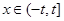 (其中
(其中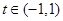 ,且
,且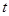 为常数)时,
为常数)时,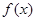 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如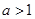 时,求满足不等式
时,求满足不等式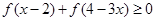 的
的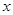 的范围.
的范围. 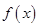 是定义在R上不恒为零的偶函数,且对任意
是定义在R上不恒为零的偶函数,且对任意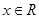 ,都有
,都有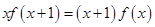 ,则
,则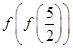 的值是( )
的值是( )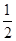
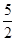
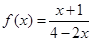 ,则
,则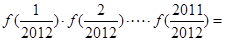 ________
________