题目内容
(本小题满分12分)
已知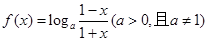
(1)求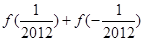 的值;
的值;
(2)当 (其中
(其中 ,且
,且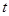 为常数)时,
为常数)时,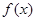 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如
果不存在,请说明理由;
(3)当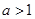 时,求满足不等式
时,求满足不等式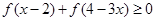 的
的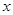 的范围.
的范围.
已知
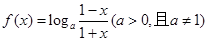
(1)求
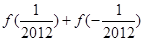 的值;
的值;(2)当
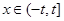 (其中
(其中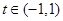 ,且
,且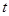 为常数)时,
为常数)时,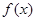 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如果不存在,请说明理由;
(3)当
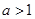 时,求满足不等式
时,求满足不等式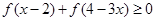 的
的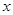 的范围.
的范围. (1) =0. (2)
=0. (2) 时,
时, 无最小值.(3)
无最小值.(3)
 =0. (2)
=0. (2) 时,
时, 无最小值.(3)
无最小值.(3)
试题分析:(1)根据所求只要判定函数的奇偶性即可,结合定义来证明。同时对于底数a进行分类讨论得到最值。
(2)结合单调性来得到函数的不等式,进而求解取值范围。
解:(1)由
 得:
得: 所以f(x)的定义域为:(-1,1),
所以f(x)的定义域为:(-1,1),又

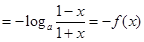 ,
,∴f(x)为奇函数,∴
 =0.
=0. (2)设
 ,
,则

∵
 ,∴
,∴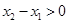 ,
, ∴
∴ ,
,当
 时
时
 ,
, 在
在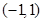 上是减函数,又
上是减函数,又
∴
 时,
时, 有最小值,且最小值为
有最小值,且最小值为
当
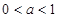 时
时
 ,
, 在
在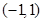 上是增函数,又
上是增函数,又
∴
 时,
时, 无最小值.
无最小值.(3)由(1)及
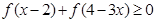 得
得
∵
 ,∴
,∴ 在
在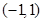 上是减函数,
上是减函数,∴
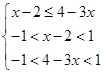 ,解得
,解得 ,∴
,∴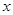 的取值范围是
的取值范围是
点评:解决该试题的关键是通过第一问的结构提示我们选择判定函数奇偶性,进而得到求解。同时对于底数a进行分类讨论得到函数的最值问题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
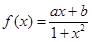 是定义在
是定义在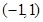 上的奇函数,且
上的奇函数,且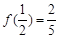 。
。 的解析式;
的解析式;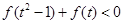 。
。
 },B={y|1
},B={y|1 },下列图形表示集合A到集合B的函数图形的是( )
},下列图形表示集合A到集合B的函数图形的是( )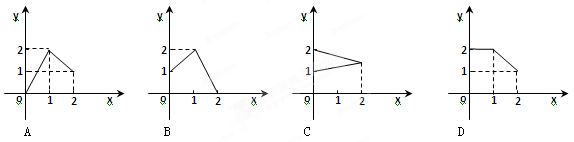
 满足
满足 .
.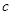 的值;
的值; 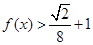 成立的x的取值范围.
成立的x的取值范围.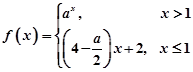 是R上的增函数,则实数
是R上的增函数,则实数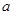 的取值范围为( )
的取值范围为( )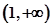
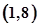
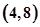
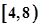
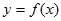 ,若同时满足下列条件:①
,若同时满足下列条件:①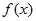 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[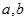 ]
]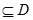 ,使
,使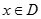 )叫闭函数.
)叫闭函数.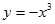 符合条件②的区间[
符合条件②的区间[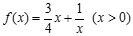 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;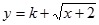 是闭函数,求实数
是闭函数,求实数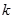 的取值范围.
的取值范围. 上市销售40天内全部售完,该公司对第一批产品
上市销售40天内全部售完,该公司对第一批产品
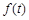 与第一批产品A上市时间t的关系式;
与第一批产品A上市时间t的关系式;