题目内容
已知椭圆 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与
的直线与 相交于
相交于 两点.若
两点.若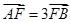 ,则
,则 ( )
( )
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与
的直线与 相交于
相交于 两点.若
两点.若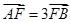 ,则
,则 ( )
( )| A.1 | B. | C. | D.2 |
B
因为 ,所以
,所以 ,从而
,从而 ,则椭圆方程为
,则椭圆方程为 。依题意可得直线方程为
。依题意可得直线方程为 ,联立
,联立 可得
可得
设 坐标分别为
坐标分别为 ,则
,则
因为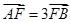 ,所以
,所以 ,从而有
,从而有 ①
①
再由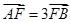 可得
可得 ,根据椭圆第二定义可得
,根据椭圆第二定义可得 ,即
,即 ②
②
由①②可得 ,所以
,所以 ,则
,则 ,解得
,解得 。因为
。因为 ,所以
,所以 ,故选B
,故选B
 ,所以
,所以 ,从而
,从而 ,则椭圆方程为
,则椭圆方程为 。依题意可得直线方程为
。依题意可得直线方程为 ,联立
,联立 可得
可得
设
 坐标分别为
坐标分别为 ,则
,则
因为
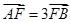 ,所以
,所以 ,从而有
,从而有 ①
①再由
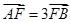 可得
可得 ,根据椭圆第二定义可得
,根据椭圆第二定义可得 ,即
,即 ②
②由①②可得
 ,所以
,所以 ,则
,则 ,解得
,解得 。因为
。因为 ,所以
,所以 ,故选B
,故选B
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
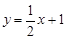 过椭圆
过椭圆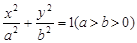 的一个焦点和一个顶点,则椭圆的离心率为( )
的一个焦点和一个顶点,则椭圆的离心率为( )
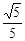
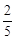
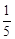
 及以下3个函数:①
及以下3个函数:①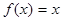 ;②
;②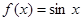 ;
;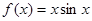 ,其中函数图像能等分该椭圆面积的函数个数有……………( ).
,其中函数图像能等分该椭圆面积的函数个数有……………( ). (
( )经过点
)经过点 ,其离心率与双曲线
,其离心率与双曲线 的离心率互为倒数.
的离心率互为倒数. 的方程;(注意椭圆的焦点在
的方程;(注意椭圆的焦点在 轴上哦!)
轴上哦!) 交椭圆
交椭圆 两点,求
两点,求 面积的最大值.
面积的最大值.
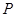 的焦点坐标为
的焦点坐标为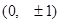 ,长轴等于焦距的2倍.
,长轴等于焦距的2倍. 的边
的边 在
在 轴上,点
轴上,点 、
、 落在椭圆
落在椭圆 的左焦点为焦点,以坐标原点为顶点的抛物线方程为( )
的左焦点为焦点,以坐标原点为顶点的抛物线方程为( )




 的左、右焦点为
的左、右焦点为 ,其上顶点为
,其上顶点为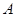 .已知
.已知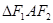 是边长为
是边长为 的正三角形.
的正三角形. 任作一直线
任作一直线 交椭圆C于
交椭圆C于 两
两 若在线段
若在线段 上取一点
上取一点 使得
使得 ,试判断当直线
,试判断当直线 是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.
是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.
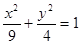 上的点,F1、F2是两个焦点,则|PF1|·|PF2|的最大值与最小值之差是_____
上的点,F1、F2是两个焦点,则|PF1|·|PF2|的最大值与最小值之差是_____ 的离心率为
的离心率为 ,则
,则 的值为_____________.
的值为_____________.