题目内容
P是椭圆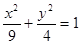 上的点,F1、F2是两个焦点,则|PF1|·|PF2|的最大值与最小值之差是_____
上的点,F1、F2是两个焦点,则|PF1|·|PF2|的最大值与最小值之差是_____
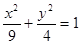 上的点,F1、F2是两个焦点,则|PF1|·|PF2|的最大值与最小值之差是_____
上的点,F1、F2是两个焦点,则|PF1|·|PF2|的最大值与最小值之差是_____5
分析:由题意,设|PF1|=x,故有|PF1|?|PF2|=x(6-x)=-x2+6x=-(x-3)2+9,
其中3-
 ≤x≤3+
≤x≤3+ 。根据 函数y=-x2+6x在(3-
。根据 函数y=-x2+6x在(3- ,3)上单调递增,(3,3+
,3)上单调递增,(3,3+ )上单调递减,可求y=-x2+6x的最小值与最大值,从而可求|PF1|?|PF2|的最大值和最小值之差。
)上单调递减,可求y=-x2+6x的最小值与最大值,从而可求|PF1|?|PF2|的最大值和最小值之差。解答:
由题意,设|PF1|=x,
∵|PF1|+|PF2|=2a=6,
∴|PF2|=6-x
∴|PF1|?|PF2|=x(6-x)=-x2+6x=-(x-3)2+9
∵椭圆c=
 ,a=3
,a=3∴3-
 ≤x≤3+
≤x≤3+
∵函数y=-x2+6x在(3-
 ,3)上单调递增,(3,3+
,3)上单调递增,(3,3+ )上单调递减,
)上单调递减,∴x=3-
 时,y=-x2+6x取最小值(3-
时,y=-x2+6x取最小值(3- )(3+
)(3+ )=4,
)=4,x=3时,y=-x2+6x取最大值为9,
∴|PF1|?|PF2|的最大值和最小值之差为9-4=5
故答案为:5
点评:本题以椭圆的标准方程为载体,考查椭圆定义的运用,考查函数的构建,考查函数的单调性,属于基础题。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与
的直线与 相交于
相交于 两点.若
两点.若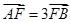 ,则
,则 ( )
( )

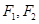 分别为椭圆
分别为椭圆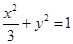 的左、右焦点,点
的左、右焦点,点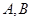 在椭圆上,若
在椭圆上,若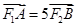 ;则点
;则点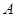 的坐标是 ______.
的坐标是 ______.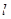 :y=kx+1(k≠0),椭圆E:
:y=kx+1(k≠0),椭圆E: ,若直线
,若直线 满分12分)已知
满分12分)已知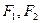 是椭圆
是椭圆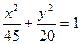 的两个焦点,
的两个焦点,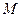 是椭圆上的点,且
是椭圆上的点,且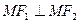 .
.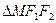 的周长;
的周长;  上有一点M,F1、F2是椭圆的左、右焦点,若
上有一点M,F1、F2是椭圆的左、右焦点,若 ,则椭圆离心率的取值范围是 )。
,则椭圆离心率的取值范围是 )。



 的焦点
的焦点 ,P为椭圆上的一点,已知
,P为椭圆上的一点,已知 ,
,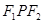 的面积为( )
的面积为( ) 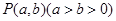 与椭圆
与椭圆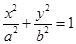 的两个焦点
的两个焦点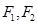 构成等腰三角形,则椭圆的离心率e= ▲
构成等腰三角形,则椭圆的离心率e= ▲ 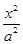 +
+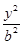 =1(a>b>0)经过点A
=1(a>b>0)经过点A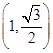 ,且离心率e=
,且离心率e=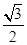 .
. O.若存在,求出直线l的方程;若不存在,说明理由.
O.若存在,求出直线l的方程;若不存在,说明理由.