题目内容
如图,已知椭圆C: 的左、右焦点为
的左、右焦点为 ,其上顶点为
,其上顶点为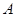 .已知
.已知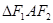 是边长为
是边长为 的正三角形.
的正三角形.
(1)求椭圆C的方程;
(2) 过点 任作一直线
任作一直线 交椭圆C于
交椭圆C于 两
两
点,记 若在线段
若在线段 上取一点
上取一点 使得
使得 ,试判断当直线
,试判断当直线 运动时,点
运动时,点 是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.
是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.

 的左、右焦点为
的左、右焦点为 ,其上顶点为
,其上顶点为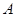 .已知
.已知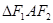 是边长为
是边长为 的正三角形.
的正三角形.(1)求椭圆C的方程;
(2) 过点
 任作一直线
任作一直线 交椭圆C于
交椭圆C于 两
两点,记
 若在线段
若在线段 上取一点
上取一点 使得
使得 ,试判断当直线
,试判断当直线 运动时,点
运动时,点 是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.
是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.
(1)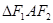 是边长为
是边长为 的正三角形,则
的正三角形,则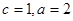 ,……………………2分
,……………………2分
故椭圆C的方程为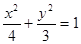 .
.  ……………………5分
……………………5分
(2)直线MN的斜率必存在,设其直线方程为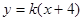 ,并设
,并设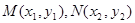 .
.
联立方程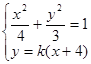 ,消去
,消去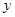 得
得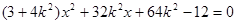 ,则
,则
 ………………8分
………………8分
由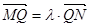 得
得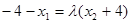 ,故
,故 . ……10分
. ……10分
设点R的坐标为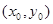 ,则由
,则由 得
得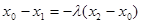 ,解得
,解得
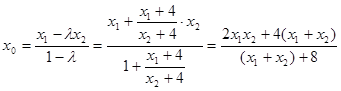 . …………………11分
. …………………11分
又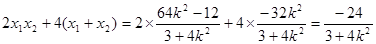 ,
,
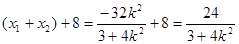 ,从而
,从而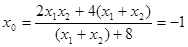 ,故点R在定直线
,故点R在定直线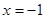 上.
上.
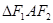 是边长为
是边长为 的正三角形,则
的正三角形,则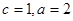 ,……………………2分
,……………………2分故椭圆C的方程为
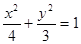 .
.  ……………………5分
……………………5分(2)直线MN的斜率必存在,设其直线方程为
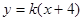 ,并设
,并设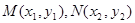 .
.联立方程
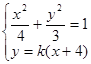 ,消去
,消去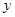 得
得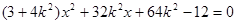 ,则
,则 ………………8分
………………8分由
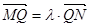 得
得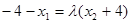 ,故
,故 . ……10分
. ……10分设点R的坐标为
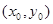 ,则由
,则由 得
得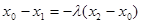 ,解得
,解得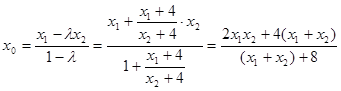 . …………………11分
. …………………11分又
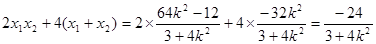 ,
, 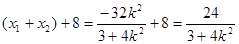 ,从而
,从而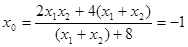 ,故点R在定直线
,故点R在定直线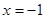 上.
上.略

练习册系列答案
相关题目
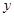 轴上的椭圆C1:
轴上的椭圆C1: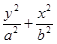 =1经过A(1,0)点,且离心率为
=1经过A(1,0)点,且离心率为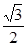 .
.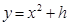 (h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与
(h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与
的直线与 相交于
相交于 两点.若
两点.若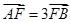 ,则
,则 ( )
( )

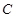 的方程为
的方程为 ,点
,点 和点
和点 (其中
(其中 和
和 均为正数)是双曲线
均为正数)是双曲线 满足
满足 (其中
(其中 ).
). 的解析式表示
的解析式表示 ;
; (
( 为坐标原点)面积的取值范围.
为坐标原点)面积的取值范围.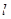 :y=kx+1(k≠0),椭圆E:
:y=kx+1(k≠0),椭圆E: ,若直线
,若直线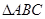 的顶点B,C在椭圆
的顶点B,C在椭圆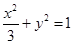 上,顶点A是椭圆的一个焦点,且椭圆的另一个焦点在BC边上,则
上,顶点A是椭圆的一个焦点,且椭圆的另一个焦点在BC边上,则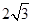
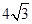
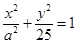 (
(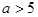 ),它的焦点分别为
),它的焦点分别为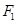 ,
,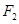 且︱
且︱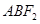 的周长为 ( )
的周长为 ( )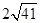 D
D 
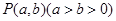 与椭圆
与椭圆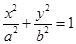 的两个焦点
的两个焦点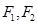 构成等腰三角形,则椭圆的离心率e= ▲
构成等腰三角形,则椭圆的离心率e= ▲ 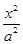 +
+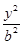 =1(a>b>0)经过点A
=1(a>b>0)经过点A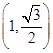 ,且离心率e=
,且离心率e=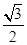 .
. O.若存在,求出直线l的方程;若不存在,说明理由.
O.若存在,求出直线l的方程;若不存在,说明理由.