题目内容
1. 已知定义域为R的函数f(x)满足f(-x)+f(x)=0,且当x>0时,f(x)=x2-2
已知定义域为R的函数f(x)满足f(-x)+f(x)=0,且当x>0时,f(x)=x2-2(1)求函数f(x)的解析式;
(2)画出函数f(x)的图象并指出它的单调区间.
(3)求函数f(x)的值域.
分析 (1)根据条件①变形,得到f(x)在定义域内是奇函数,设x小于0,得到-x大于0,代入②中f(x)的解析式中化简后即可得到x小于0时f(x)的解析式,综上,得到f(x)在x大于0和小于0上的分段函数解析式;当x=0时f(x)=0;
(2)分段画出f(x)的图象.
(3)由图象可知函数的值域.
解答 解:(1)∵对于f(x)定义域内的任意实数x,都有f(-x)+f(x)=0,
∴f(-x)=-f(x),
故f(x)在其定义域R内是奇函数,
所以f(0)=0
∵当x>0时,f(x)=x2-2,
设x<0,所以-x>0,
∴f(-x)=-f(x)=x2-2,即f(x)=2-x2,
则 f(x)=$\left\{\begin{array}{l}{{x}^{2}-2,x>0}\\{0,x=0}\\{2-{x}^{2},x<0}\end{array}\right.$;
(2)函数f(x)的图象为: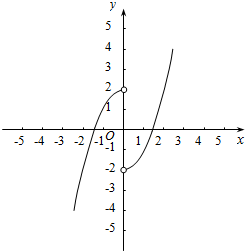
(3)由图象可知,值域为R.
点评 此题要求学生掌握奇函数的性质及确定方法,考查了一元二次不方程的解法,考查了分类讨论的数学思想,是一道中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
11.已知集合A={1,3,x},B={x2,1},由集合A与B的所有元素组成集合{1,3,x},这样的实数x共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.已知集合A满足条件{1,2}⊆A?{1,2,3,4,5},则集合A的个数有( )
| A. | 8 | B. | 7 | C. | 4 | D. | 3 |
10.已知y=f(x+1)是R上的偶函数,且f(2)=1,则f(0)=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
11.在等差数列{an}中,已知a2+a20=10,则S21等于( )
| A. | 0 | B. | 100 | C. | 105 | D. | 200 |
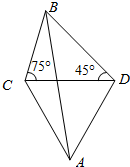 如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.
如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.