题目内容
9.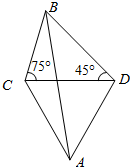 如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.
如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.
分析 由三角形内角和定理得出∠CBD=60°,在△BCD中,由正弦定理得出BD,再在△ABD中利用余弦定理解出AB即可.
解答 解:∠CBD=180°-∠CDB-∠BCD=180°-45°-75°=60°,
在△BCD中,由正弦定理,得:
BD=$\frac{CDsin75°}{sin60°}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
在△ABD中,∠ADB=45°+60°=105°,
由余弦定理,得AB2=AD2+BD2-2AD•BDcos105°
=3+($\frac{\sqrt{6}+\sqrt{2}}{2}$)2-2×$\sqrt{3}$×$\frac{\sqrt{6}+\sqrt{2}}{2}$×$\frac{\sqrt{2}-\sqrt{6}}{4}$=5+2$\sqrt{3}$.
∴AB=$\sqrt{5+2\sqrt{3}}$.
答:炮兵阵地与目标的距离为$\sqrt{5+2\sqrt{3}}$km
点评 本题考查了解三角形的实际应用,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
19.定义:若复数z与z1满足z•z1=1,则称复数z与z1互为倒数,已知复数z=i(2+3i),则复数z的倒数z1为( )
| A. | -$\frac{3}{13}+\frac{2}{13}$i | B. | -$\frac{3}{13}-\frac{2}{13}$i | C. | $\frac{3}{13}+\frac{2}{13}$i | D. | $\frac{3}{13}-\frac{2}{13}$i |
14.已知两个不同的平面α、β和两条不重合的直线m、n,有下列四个命题:
①若m∥n,m⊥α,则n⊥α;
②若m⊥α,m⊥β,则α∥β;
③若m∥n,n?α,则m∥α;
④若m∥α,α∩β=n,则m∥n.
其中正确命题的个数是( )
①若m∥n,m⊥α,则n⊥α;
②若m⊥α,m⊥β,则α∥β;
③若m∥n,n?α,则m∥α;
④若m∥α,α∩β=n,则m∥n.
其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 已知定义域为R的函数f(x)满足f(-x)+f(x)=0,且当x>0时,f(x)=x2-2
已知定义域为R的函数f(x)满足f(-x)+f(x)=0,且当x>0时,f(x)=x2-2