题目内容
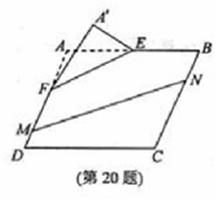
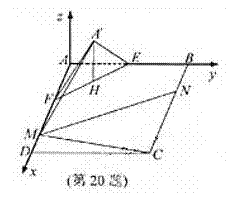
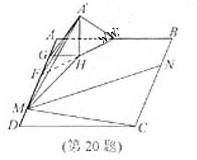
本题满分15分)如图,在矩形
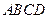 中,点
中,点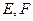 分别
分别在线段
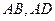 上,
上,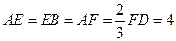 .沿直线
.沿直线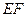
将
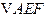 翻折成
翻折成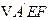 ,使平面
,使平面 .
.
(Ⅰ)求二面角
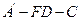 的余弦值;
的余弦值;(Ⅱ)点
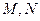 分别在线段
分别在线段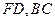 上,若沿直线
上,若沿直线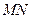 将四
将四边形
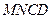 向上翻折,使
向上翻折,使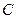 与
与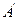 重合,求线段
重合,求线段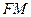
的长。
 ,
,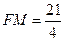
(Ⅰ)解:取线段EF的中点H,连结 ,因为
,因为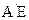 =
=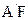 及H是EF的中点,所以
及H是EF的中点,所以 ,
,
又因为平面 平面
平面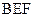 .
.
如图建立空间直角坐标系A-xyz
则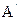 (2,2,
(2,2,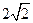 ),C(10,8,0),
),C(10,8,0),
F(4,0,0),D(10,0,0).
故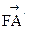 =(-2,2,2
=(-2,2,2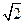 ),
),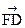 =(6,0,0).
=(6,0,0).
设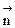 =(x,y,z)为平面
=(x,y,z)为平面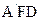 的一个法向量,
的一个法向量,
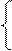 -2x+2y+2
-2x+2y+2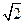 z=0
z=0
所以
6x=0.
取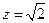 ,则
,则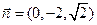 。
。
又平面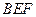 的一个法向量
的一个法向量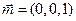 ,
,
故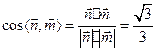 。
。
所以二面角的余弦值为
(Ⅱ)解:设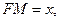 则
则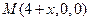 ,
,
因为翻折后,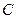 与
与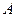 重合,所以
重合,所以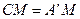 ,
,
故,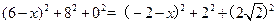 ,得
,得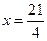 ,
,
经检验,此时点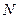 在线段
在线段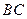 上,
上,
所以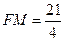 。
。
方法二:
(Ⅰ)解:取线段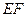 的中点
的中点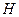 ,
,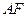 的中点
的中点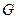 ,连结
,连结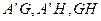 。
。
因为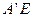 =
=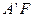 及
及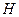 是
是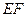 的中点,
的中点,
所以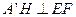
又因为平面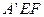
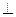 平面
平面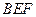 ,
,
所以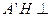 平面
平面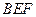 ,
,
又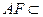 平面
平面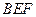 ,
,
故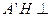
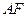 ,
,
又因为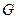 、
、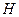 是
是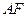 、
、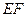 的中点,
的中点,
易知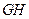 ∥
∥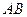 ,
,
所以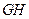
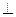
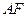 ,
,
于是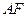
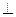 面
面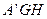 ,
,
所以 为二面角
为二面角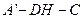 的平面角,
的平面角,
在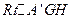 中,
中,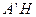 =
=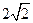 ,
,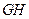 =2,
=2,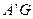 =
=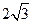
所以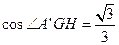 .
.
故二面角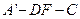 的余弦值为
的余弦值为 。
。
(Ⅱ)解:设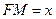 ,
,
因为翻折后,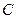 与
与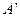 重合,
重合,
所以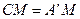 ,
,
而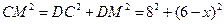 ,
,
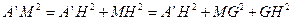
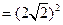
得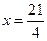 ,
,
经检验,此时点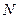 在线段
在线段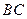 上,
上,
所以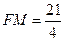 。
。
 ,因为
,因为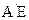 =
=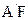 及H是EF的中点,所以
及H是EF的中点,所以 ,
,

又因为平面
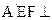 平面
平面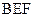 .
.如图建立空间直角坐标系A-xyz
则
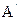 (2,2,
(2,2,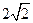 ),C(10,8,0),
),C(10,8,0),F(4,0,0),D(10,0,0).
故
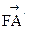 =(-2,2,2
=(-2,2,2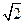 ),
),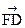 =(6,0,0).
=(6,0,0).设
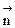 =(x,y,z)为平面
=(x,y,z)为平面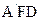 的一个法向量,
的一个法向量,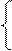 -2x+2y+2
-2x+2y+2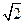 z=0
z=0所以
6x=0.
取
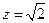 ,则
,则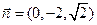 。
。又平面
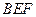 的一个法向量
的一个法向量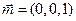 ,
,故
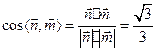 。
。所以二面角的余弦值为

(Ⅱ)解:设
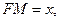 则
则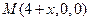 ,
,因为翻折后,
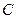 与
与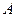 重合,所以
重合,所以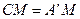 ,
,故,
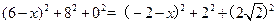 ,得
,得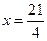 ,
,经检验,此时点
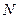 在线段
在线段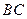 上,
上,所以
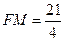 。
。方法二:
(Ⅰ)解:取线段
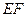 的中点
的中点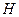 ,
,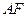 的中点
的中点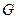 ,连结
,连结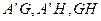 。
。因为
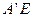 =
=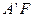 及
及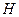 是
是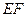 的中点,
的中点,所以
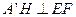
又因为平面
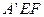
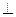 平面
平面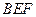 ,
,所以
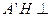 平面
平面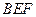 ,
,又
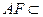 平面
平面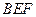 ,
,故
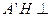
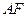 ,
,又因为
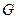 、
、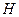 是
是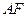 、
、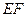 的中点,
的中点,易知
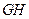 ∥
∥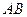 ,
,所以
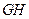
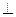
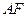 ,
,于是
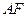
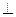 面
面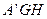 ,
,所以
 为二面角
为二面角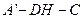 的平面角,
的平面角,在
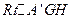 中,
中,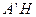 =
=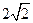 ,
,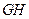 =2,
=2,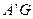 =
=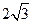
所以
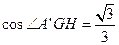 .
.故二面角
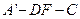 的余弦值为
的余弦值为 。
。(Ⅱ)解:设
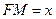 ,
,因为翻折后,
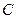 与
与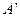 重合,
重合,所以
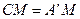 ,
,而
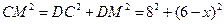 ,
,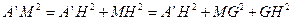
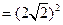
得
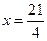 ,
,经检验,此时点
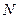 在线段
在线段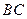 上,
上,所以
 。
。
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
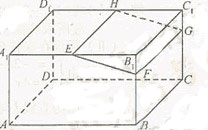
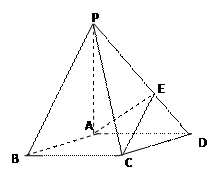 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=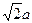 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.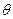 的大小.
的大小.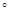 的二面角,这时A到边BC的距离是( )
的二面角,这时A到边BC的距离是( )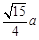
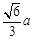
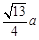
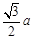
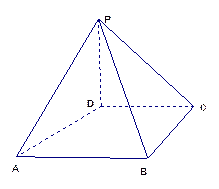
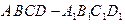 中,底面是边长为
中,底面是边长为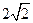 的正方形,侧棱长为4。
的正方形,侧棱长为4。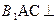 平面
平面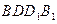 ;
;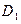 到平面
到平面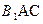 的距离d;
的距离d;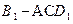 的体积V。
的体积V。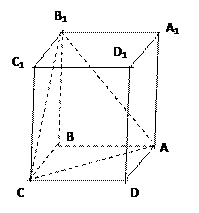
 、
、 、
、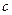 表示三条不同的直线,
表示三条不同的直线,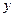 表示平面,给出下列命题:
表示平面,给出下列命题: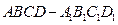 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点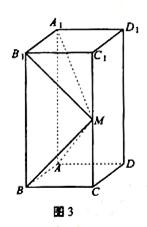
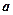 、
、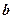 及平面
及平面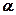 ,给出四个下列命题:
,给出四个下列命题: ,
,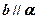 ,则
,则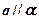 ;
;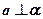 ,
,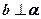 ,则
,则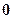 个
个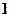 个
个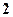 个
个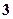 个
个