题目内容
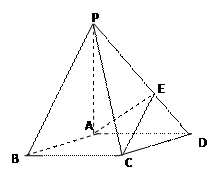 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=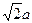 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.(Ⅰ)证明PA⊥平面ABCD;
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角
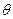 的大小.
的大小.
|
(Ⅰ)证明: 因为底面ABCD是菱形,∠ABC=60°,
所以AB=AD=AC=a, 在△PAB中,
由PA2+AB2=2a2=PB2 知PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD
(II)解:作EG//PA交AD于G,
由PA⊥平面ABCD.
知EG⊥平面ABCD.作GH⊥AC于H,连结EH,则EH⊥AC,∠EHG即为二面角
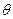 的平面角.
的平面角.又PE : ED="2" : 1,所以

从而
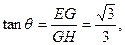
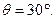

练习册系列答案
相关题目
 B
B 平面ABCD,底面ABCD是边长为1的正方形,侧棱AA
平面ABCD,底面ABCD是边长为1的正方形,侧棱AA
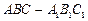 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是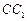 的中点,直线
的中点,直线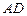 与侧面
与侧面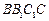 所成的角是
所成的角是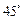 .
.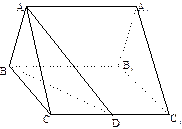
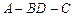 的大小;
的大小;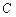 到平面
到平面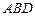 的距离.
的距离.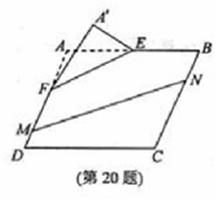
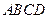 中,点
中,点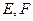 分别
分别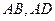 上,
上,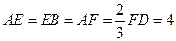 .沿直线
.沿直线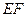
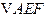 翻折成
翻折成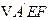 ,使平面
,使平面 .
.
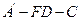 的余弦值;
的余弦值;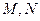 分别在线段
分别在线段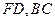 上,若沿直线
上,若沿直线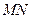 将四
将四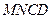 向上翻折,使
向上翻折,使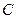 与
与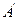 重合,求线段
重合,求线段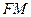
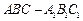 中,侧面
中,侧面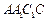
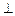 底面
底面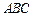 ,
,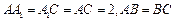 ,
, ,O为
,O为 中点.
中点.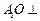 平面
平面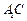 与平面
与平面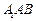 所成角的正弦值;
所成角的正弦值;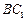 上是否存在一点
上是否存在一点 ,使得
,使得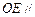 平面
平面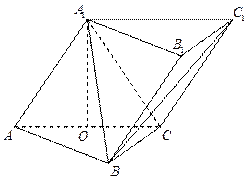
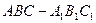 中,
中,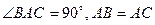 ,直线
,直线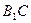 与平面
与平面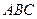 成
成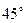 角;
角;
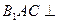 平面
平面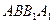 ;
;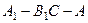 的正弦值.
的正弦值.
 平面ABC ,
平面ABC ,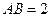 ,
,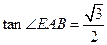 .
.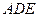 ;
;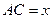 ,
, 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求
 (3)当
(3)当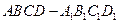 中,
中,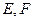 分别为棱
分别为棱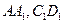 的中点,
的中点,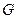 是侧面
是侧面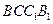 的中心,则空间四边形
的中心,则空间四边形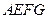 在正方体的六个面上的射影图形面积的最大值是( )
在正方体的六个面上的射影图形面积的最大值是( )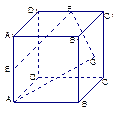
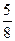
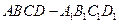 的棱长为3,点
的棱长为3,点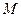 在
在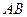 上,且
上,且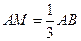 ,点
,点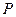 在平面
在平面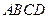 上,且动点
上,且动点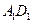 的距离与
的距离与 中,动点
中,动点