题目内容
已知两条不同的直线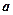 、
、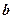 及平面
及平面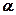 ,给出四个下列命题:
,给出四个下列命题:
(1)若 ,
,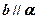 ,则
,则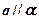 ;
;
(2)若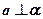 ,
,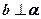 ,则
,则 ;
;
(3)若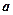 、
、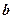 与
与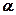 所成的角相等,则
所成的角相等,则 ;
;
(4)若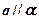 ,
,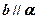 ,则
,则 .
.
其中正确的命题有( )
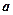 、
、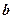 及平面
及平面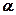 ,给出四个下列命题:
,给出四个下列命题:(1)若
 ,
,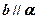 ,则
,则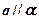 ;
;(2)若
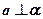 ,
,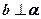 ,则
,则 ;
;(3)若
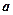 、
、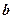 与
与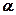 所成的角相等,则
所成的角相等,则 ;
;(4)若
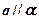 ,
,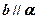 ,则
,则 .
.其中正确的命题有( )
A.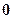 个 个 | B.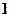 个 个 | C.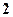 个 个 | D.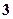 个 个 |
B
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
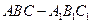 中,
中,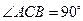 ,
,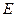 是棱
是棱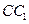 上的动点,
上的动点,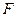 是
是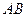 中点,
中点,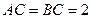 ,
,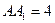 .
.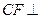 平面
平面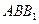 ;
;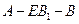 的大小是
的大小是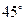 ,求
,求 的长.
的长.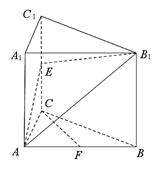
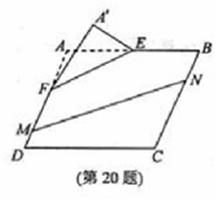
 中,点
中,点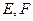 分别
分别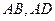 上,
上,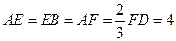 .沿直线
.沿直线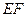
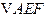 翻折成
翻折成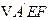 ,使平面
,使平面 .
.
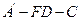 的余弦值;
的余弦值;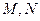 分别在线段
分别在线段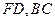 上,若沿直线
上,若沿直线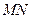 将四
将四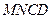 向上翻折,使
向上翻折,使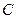 与
与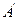 重合,求线段
重合,求线段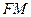
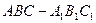 中,
中,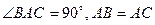 ,直线
,直线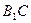 与平面
与平面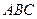 成
成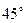 角;
角;
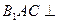 平面
平面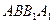 ;
;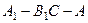 的正弦值.
的正弦值.
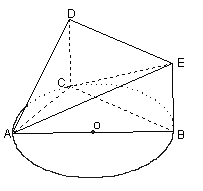
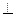 平面ABC ,
平面ABC ,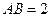 ,
,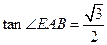 .
.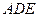 ;
;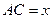 ,
,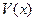 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求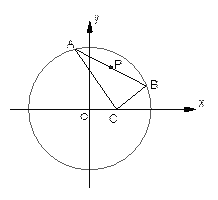
 (3)当
(3)当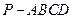 中,底面为菱形,
中,底面为菱形,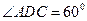 ,
,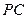 与底面
与底面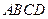 垂直,
垂直,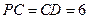 ,
,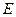 为棱
为棱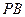 的中点,
的中点,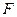 为
为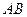 的中点,
的中点,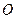 为
为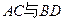 的交点,
的交点,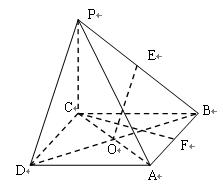
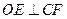 ;
;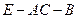 的余弦值.
的余弦值.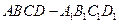 的棱长为3,点
的棱长为3,点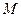 在
在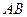 上,且
上,且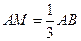 ,点
,点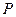 在平面
在平面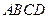 上,且动点
上,且动点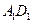 的距离与
的距离与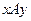 中,动点
中,动点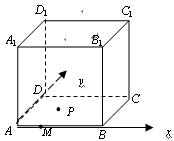
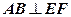
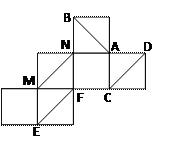 ;
;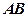 与
与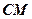 成
成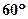 角;
角;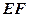 与
与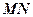 是异面直线;
是异面直线;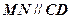 .
.