题目内容
(本小题满分12分)
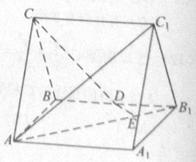
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1 D1. 过EH的平面与棱BB1,CC1相交,交点分别为F,G。
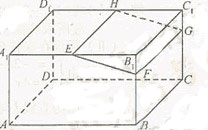
(I) 证明:AD∥平面EFGH;
(II) 设AB=2AA1 ="2" a .在长方体ABCD-A1B1C1D1内随机选取一点。记该点取自几何体A1ABFE-D1DCGH内的概率为p,当点E,F分别在棱A1B1上运动且满足EF=a时,求p的最小值.
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1 D1. 过EH的平面与棱BB1,CC1相交,交点分别为F,G。

(I) 证明:AD∥平面EFGH;
(II) 设AB=2AA1 ="2" a .在长方体ABCD-A1B1C1D1内随机选取一点。记该点取自几何体A1ABFE-D1DCGH内的概率为p,当点E,F分别在棱A1B1上运动且满足EF=a时,求p的最小值.
(I)见解析(II)p的最小值等于7/8
本小题主要考察直线与直线、直线与平面的位置关系,以及几何体的体积、几何概念等基础知识,考察空间想象能力、推理论证能力、运算求解能力,考察函数与方程思想、形数结合思想、化归与转化思想、必然与或然思想。满分12分
解法一:
(I) 证明:在长方体ABCD-A1B1C1D1中,AD∥A1 D1
又∵EH∥A1 D1 ,∴AD∥EH.
,∴AD∥EH.
∵AD¢平面EFGH
EH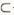 平面EFGH
平面EFGH
∴AD//平面EFGH.
(II) 设BC=b,则长方体ABCD-A1B1C1D1的体积V=AB·AD·AA1 =2a2b,
几何体EB1F-HC1G的体积V1 =(1/2EB1 ·B1F)·B1C1 =b/2·EB1 ·B1 F
∵EB12 + B1 F2=a2
∴EB12 + B1 F2≤ (E B12 + B1 F2)/2 = a2 / 2,当且仅当EB1
B12 + B1 F2)/2 = a2 / 2,当且仅当EB1 =B1 F=
=B1 F= a时等号成立
a时等号成立
从而V1 ≤ a2b /4 .
故 p=1-V1/V ≥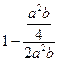 =
=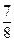
解法二:
(I) 同解法一
(II) 设BC=b,则长方体ABCD-A1B1C1D1的体积V=AB·AD·AA1 =2a2b ,
几何体EB1F-HC1G的体积
V1=(1/2 EB1 ·B1 F)·B1C1 =b/2 EB1 ·B1 F
设∠B1EF=θ(0°≤θ≤90°),则EB1 =" a" cosθ,B1 F ="a" sinθ
故EB1 ·B1 F = a2 sinθcosθ=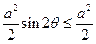 ,当且仅当sin 2θ=1即θ=45°时等号成立.
,当且仅当sin 2θ=1即θ=45°时等号成立.
从而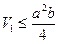
∴p=1- V1/V≥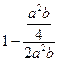 =
=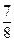 ,当且仅当sin 2θ=1即θ=45°时等号成立.
,当且仅当sin 2θ=1即θ=45°时等号成立.
所以,p的最小值等于7/8
解法一:
(I) 证明:在长方体ABCD-A1B1C1D1中,AD∥A1 D1
又∵EH∥A1 D1
 ,∴AD∥EH.
,∴AD∥EH.∵AD¢平面EFGH
EH
 平面EFGH
平面EFGH∴AD//平面EFGH.
(II) 设BC=b,则长方体ABCD-A1B1C1D1的体积V=AB·AD·AA1 =2a2b,
几何体EB1F-HC1G的体积V1 =(1/2EB1 ·B1F)·B1C1 =b/2·EB1 ·B1 F
∵EB12 + B1 F2=a2
∴EB12 + B1 F2≤ (E
 B12 + B1 F2)/2 = a2 / 2,当且仅当EB1
B12 + B1 F2)/2 = a2 / 2,当且仅当EB1 =B1 F=
=B1 F= a时等号成立
a时等号成立从而V1 ≤ a2b /4 .
故 p=1-V1/V ≥
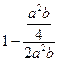 =
=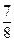
解法二:
(I) 同解法一
(II) 设BC=b,则长方体ABCD-A1B1C1D1的体积V=AB·AD·AA1 =2a2b ,
几何体EB1F-HC1G的体积
V1=(1/2 EB1 ·B1 F)·B1C1 =b/2 EB1 ·B1 F
设∠B1EF=θ(0°≤θ≤90°),则EB1 =" a" cosθ,B1 F ="a" sinθ
故EB1 ·B1 F = a2 sinθcosθ=
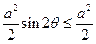 ,当且仅当sin 2θ=1即θ=45°时等号成立.
,当且仅当sin 2θ=1即θ=45°时等号成立.从而
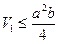
∴p=1- V1/V≥
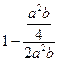 =
=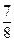 ,当且仅当sin 2θ=1即θ=45°时等号成立.
,当且仅当sin 2θ=1即θ=45°时等号成立.所以,p的最小值等于7/8

练习册系列答案
相关题目
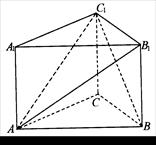
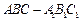 中,
中,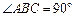 ,
,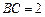 ,
,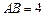 ,
,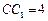 ,E在
,E在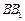 上,且
上,且 ,
,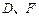 分别为
分别为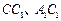 的中点.
的中点.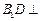 平面
平面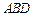 ;
;  与
与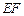 所成的角;
所成的角;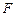 到平面
到平面
 B
B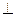 平面ABCD,底面ABCD是边长为1的正方形,侧棱AA
平面ABCD,底面ABCD是边长为1的正方形,侧棱AA
 中,
中,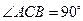 ,
,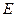 是棱
是棱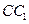 上的动点,
上的动点,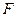 是
是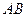 中点,
中点,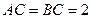 ,
,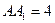 .
.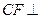 平面
平面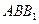 ;
;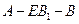 的大小是
的大小是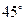 ,求
,求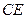 的长.
的长.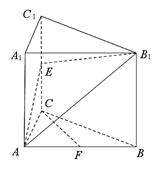
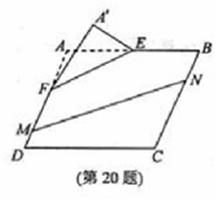
 中,点
中,点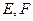 分别
分别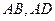 上,
上,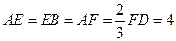 .沿直线
.沿直线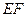
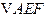 翻折成
翻折成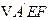 ,使平面
,使平面 .
.
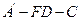 的余弦值;
的余弦值;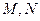 分别在线段
分别在线段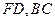 上,若沿直线
上,若沿直线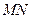 将四
将四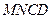 向上翻折,使
向上翻折,使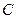 与
与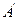 重合,求线段
重合,求线段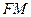
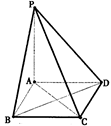
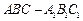 中,侧面
中,侧面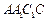
 底面
底面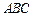 ,
,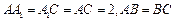 ,
, ,O为
,O为 中点.
中点.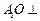 平面
平面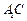 与平面
与平面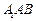 所成角的正弦值;
所成角的正弦值;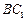 上是否存在一点
上是否存在一点 ,使得
,使得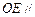 平面
平面
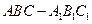 中,
中,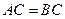 ,
,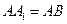 ,
,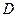 为
为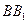 的中点,
的中点,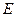 为
为 上的一点,
上的一点,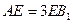 .
.
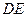 为异面直线
为异面直线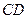 的公垂线;
的公垂线;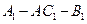 的大小.
的大小.