题目内容
用 、
、 、
、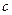 表示三条不同的直线,
表示三条不同的直线,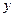 表示平面,给出下列命题:
表示平面,给出下列命题:
①若 ∥
∥ ,
, ∥
∥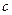 ,则
,则 ∥
∥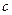 ;②若
;②若 ⊥
⊥ ,
, ⊥
⊥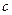 ,则
,则 ⊥
⊥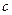 ;
;
③若 ∥
∥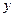 ,
, ∥
∥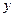 ,则
,则 ∥
∥ ;④若
;④若 ⊥
⊥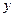 ,
, ⊥
⊥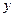 ,则
,则 ∥
∥ .
.
 、
、 、
、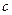 表示三条不同的直线,
表示三条不同的直线,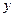 表示平面,给出下列命题:
表示平面,给出下列命题:①若
 ∥
∥ ,
, ∥
∥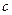 ,则
,则 ∥
∥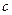 ;②若
;②若 ⊥
⊥ ,
, ⊥
⊥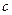 ,则
,则 ⊥
⊥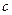 ;
;③若
 ∥
∥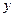 ,
, ∥
∥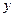 ,则
,则 ∥
∥ ;④若
;④若 ⊥
⊥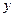 ,
, ⊥
⊥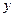 ,则
,则 ∥
∥ .
.| A.①② | B.②③ | C.①④ | D.③④ |
C
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
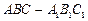 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是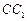 的中点,直线
的中点,直线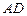 与侧面
与侧面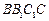 所成的角是
所成的角是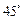 .
.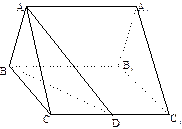
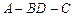 的大小;
的大小;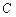 到平面
到平面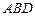 的距离.
的距离.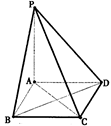
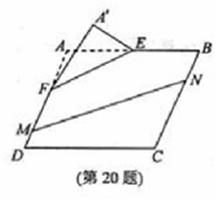
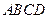 中,点
中,点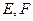 分别
分别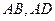 上,
上,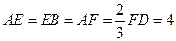 .沿直线
.沿直线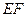
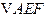 翻折成
翻折成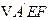 ,使平面
,使平面 .
.
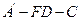 的余弦值;
的余弦值;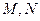 分别在线段
分别在线段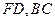 上,若沿直线
上,若沿直线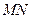 将四
将四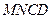 向上翻折,使
向上翻折,使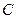 与
与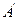 重合,求线段
重合,求线段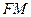
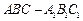 中,侧面
中,侧面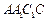
 底面
底面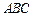 ,
,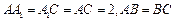 ,
, ,O为
,O为 中点.
中点.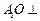 平面
平面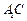 与平面
与平面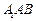 所成角的正弦值;
所成角的正弦值;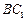 上是否存在一点
上是否存在一点 ,使得
,使得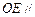 平面
平面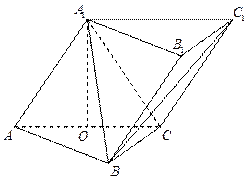
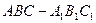 中,
中,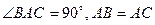 ,直线
,直线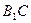 与平面
与平面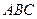 成
成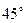 角;
角;
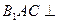 平面
平面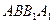 ;
;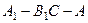 的正弦值.
的正弦值.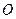 的半径为1,
的半径为1,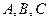 三点都在球面上,且每两点间的球面距离均为
三点都在球面上,且每两点间的球面距离均为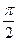 ,则球心
,则球心 的距离为
的距离为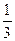
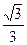
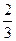
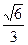
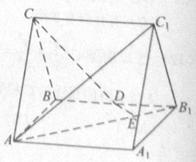
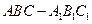 中,
中,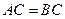 ,
,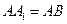 ,
,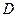 为
为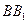 的中点,
的中点,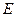 为
为 上的一点,
上的一点,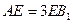 .
.
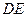 为异面直线
为异面直线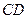 的公垂线;
的公垂线;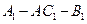 的大小.
的大小.