题目内容
13.设棱锥M-ABCD的底面是正方形,且MA=AD,MA⊥平面ABCD,如果△AMD面积为2,试求能够放入这个棱锥的最大球的半径.分析 设球O是与平面MAB、平面AC、平面MDC都相切的球.然后找出球心所在的三角形,由面积求得AD=EF=2,求出内切圆半径即可求出最大值.
解答 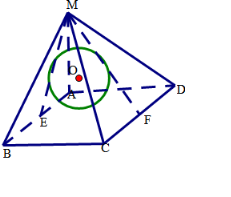 解:由MA⊥平面ABCD,MA=AD,△AMD面积为2,
解:由MA⊥平面ABCD,MA=AD,△AMD面积为2,
即有MA⊥AD,$\frac{1}{2}$AM•AD=2,解得AD=2,
CD⊥AD,MA⊥CD,则有CD⊥平面MAD,即有CD⊥MD,
记E是AB的中点,从而ME=$\sqrt{4+1}$=$\sqrt{5}$.
EF=2,MF=$\sqrt{4+4+1}$=3,
设球O是与平面MAB、平面AC、平面MDC都相切的球.
不妨设O∈平面MEF,于是O是△MEF的内心.
设球O的半径为r,则r=$\frac{2{S}_{△MEF}}{EF+EM+MF}$,
r=$\frac{2×\frac{1}{2}×2\sqrt{5}}{2+3+\sqrt{5}}$=$\frac{\sqrt{5}-1}{2}$.
则能够放入这个棱锥的最大球的半径为$\frac{\sqrt{5}-1}{2}$.
点评 涉及球与棱柱、棱锥的切接问题时一般过球心及多面体中的特殊点或线作截面,把空间问题化归为平面问题,再利用平面几何知识寻找几何体中元素间的关系,注意多边形内切圆半径与面积和周长间的关系;多面体内切球半径与体积和表面积间的关系,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1、F2,离心率为$\frac{1}{2}$,过点F1的直线l交椭圆于A、B两点,△AF2B的周长为8.
椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1、F2,离心率为$\frac{1}{2}$,过点F1的直线l交椭圆于A、B两点,△AF2B的周长为8.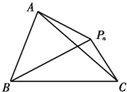 如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )
如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )