题目内容
5.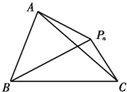 如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )
如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )| A. | 15 | B. | 17 | C. | 33 | D. | 31 |
分析 由$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$可得$\overrightarrow{{P_n}A}$+(2xn+1)$\overrightarrow{{P_n}C}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$,画出图形后利用三角形面积的关系得到数列递推式,然后构造等比数列得答案
解答 解:由$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$得$\overrightarrow{{P_n}A}$+(2xn+1)$\overrightarrow{{P_n}C}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$,
设$\overrightarrow{{P}_{n}D}$=(2${x}_{n}+1)\overrightarrow{{P}_{n}C}$$\overrightarrow{{P}_{n}C}$,
以线段PnA、PnD作出平行四边形AEDPn,如图,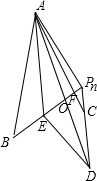
则$\overrightarrow{{P}_{n}A}+\overrightarrow{{P}_{n}D}=\overrightarrow{{P}_{n}E}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$,
∴$\frac{|\overrightarrow{{P}_{n}E}|}{|\overrightarrow{{P}_{n}B}|}=\frac{{x}_{n+1}}{3}$,∴$\frac{{S}_{△{P}_{n}AE}}{{S}_{△{P}_{n}AB}}=\frac{{x}_{n+1}}{3}$,
∵$\frac{|\overrightarrow{{P}_{n}C}|}{|\overrightarrow{{P}_{n}D}|}=\frac{|\overrightarrow{{P}_{n}C}|}{AE}=\frac{1}{2{x}_{n}+1}$,
∴$\frac{{S}_{△{P}_{n}AC}}{{S}_{△{P}_{n}AD}}=\frac{{S}_{△{P}_{n}AC}}{{S}_{△{P}_{n}AE}}=\frac{1}{1+2{x}_{n}}$,
则$\frac{{S}_{△{P}_{n}AC}}{{S}_{△{P}_{n}AB}}$=$\frac{{x}_{n+1}}{3(1+2{x}_{n})}=\frac{1}{3}$,
即xn+1=2xn+1,∴xn+1+1=2(xn+1),
则{xn+1}构成以2为首项,以2为公比的等比数列,所以x4+1=2×23=16,所以x4=15;
故选A.
点评 本题考查了平面向量的三角形法则,考查了数学转化思想方法,训练了利用构造法构造等比数列,考查了计算能力,属于难题.

| A. | 22 | B. | 564.9 | C. | 20 | D. | 14130.2 |
| A. | a≤1 | B. | a≥1 | C. | a≥$\frac{3}{2}$ | D. | a≤$\frac{3}{2}$ |