题目内容
3.已知双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{{{a^2}-4}}$=1(a>2).(1)若E的离心率为$\frac{{\sqrt{14}}}{3}$,求E的方程;
(2)设E的左、右焦点为F1、F2,点P为双曲线上的点,直线F2P交y轴于点Q,并且F1P⊥F1Q,当a变化时,若点P是第一象限内的点,则点P在某一条定直线上吗?如果这条定直线存在,请求出直线方程;如果不存在这条定直线,请说明理由.
分析 (1)利用双曲线的离心率,解得a=3,然后求出椭圆E的方程.
(2)假设这条定直线存在.设P(x,y)、Q(0,yQ),利用F1P⊥F1Q,推出x2-y2=2a2-4,与双曲线方程联立,然后求出直线方程.
解答 (1)解:$e=\frac{{\sqrt{{a^2}+({a^2}-4)}}}{a}=\frac{{\sqrt{14}}}{3}$,…(2分)
解得:a2=9…(3分)
∵a>0,∴a=3…(4分)
E:$\frac{x^2}{9}-\frac{y^2}{5}=1$…(5分)
(2)解:假设这条定直线存在.
设P(x,y)、Q(0,yQ),而$c=\sqrt{2{a^2}-4}$,F1(-c,0)、F2(c,0)
由P、F2、Q三点共线知$\frac{{y-{y_Q}}}{x}=\frac{y}{x-c}(x≠c,x≠0)$,…(6分)
即${y_Q}=\frac{-yc}{y-c}$,…(7分)
所以$\overrightarrow{{F}_{1}P}$=(x+c,y),$\overrightarrow{{F}_{1}Q}$=$(c,\frac{-yc}{x-c})$…(8分)
因为F1P⊥F1Q,所以$\overrightarrow{{F}_{1}P}•\overrightarrow{{F}_{1}Q}$=$xc+{c}^{2}-\frac{{y}^{2}c}{x-c}=0$,…(9分)
故x2-y2=c2,即x2-y2=2a2-4,…(10分)
与双曲线方程联立得:$\left\{\begin{array}{l}{x^2}-{y^2}=2{a^2}-4\\ \frac{x^2}{a^2}-\frac{y^2}{{{a^2}-4}}=1\end{array}\right.$
解得${x^2}=\frac{a^4}{4}$,${y^2}=\frac{{{{({a^2}-4)}^2}}}{4}$,…(12分)
若点P为第一象限内的点,则x>0,y>0,
所以$x=\frac{a^2}{2}$,$y=\frac{{{a^2}-4}}{2}$,…(13分)
∴x-y=2,
即点P在定直线x-y=2上.…(14分)
点评 本题考查直线与双曲线的位置关系的综合应用,双曲线方程的求法,考查分析问题解决问题的能力.

 阅读快车系列答案
阅读快车系列答案| A. | -$\frac{4}{5}$i | B. | $\frac{4}{5}$i | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
| A. | (-1,7) | B. | (-∞,-7)U(-1,+∞) | C. | (-7,1) | D. | (-∞,1)U(7,+∞) |
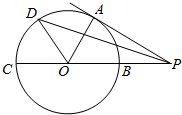 如图,PA切⊙O于点A,割线PBC经过圆心O,PB=1,PA=$\sqrt{3}$,OA绕点O逆时针旋转60°到OD,则PD的长为$\sqrt{7}$.
如图,PA切⊙O于点A,割线PBC经过圆心O,PB=1,PA=$\sqrt{3}$,OA绕点O逆时针旋转60°到OD,则PD的长为$\sqrt{7}$.