Question

3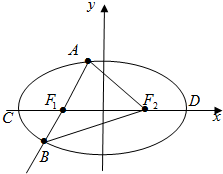．椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点为F₁、F₂，离心率为$\frac{1}{2}$，过点F₁的直线l交椭圆于A、B两点，△AF₂B的周长为8．
（1）求椭圆方程．
（2）若椭圆的左、右顶点为C、D，四边形ABCD的面积为$\frac{{24\sqrt{2}}}{7}$，求直线l的方程．

Answer 1

分析 （1）由题意结合椭圆定义求得a，再由椭圆离心率求得c，结合隐含条件求得b，则椭圆方程可求；
（2）设出直线l的方程，联立直线方程和椭圆方程，化为关于y的一元二次方程，利用根与系数的关系求得A，B两点纵坐标差的绝对值，由四边形ABCD的面积列式求得直线的斜率，则直线l的方程可求．

解答 解：（1）∵|AF₁|+|AF₂|=2a，|BF₁|+|BF₂|=2a，
∴|AF₂|+|BF₂|+|AB|=4a，即4a=8，则a=2．
又∵e=$\frac{c}{a}$=$\frac{1}{2}$，∴c=1，则b²=a²-c²=3．
∴椭圆方程为$\frac{x^2}{4}$+$\frac{y^2}{3}$=1；
（2）设直线l的方程为x=ky-1，
代入椭圆方程并化简得（3k²+4）y²-6ky-9=0，
设A（x₁，y₁）、B（x₂，y₂），
则${y}_{1}+{y}_{2}=\frac{6k}{3{k}^{2}+4}，{y}_{1}{y}_{2}=\frac{-9}{3{k}^{2}+4}$，
∴|y₁-y₂|=$\sqrt{（{y}_{1}+{y}_{2}）^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{（\frac{6k}{3{k}^{2}+4}）^{2}+\frac{36}{3{k}^{2}4}}$=$\frac{{\sqrt{36{k^2}+36（{3{k^2}+4}）}}}{{3{k^2}+4}}=\frac{{12\sqrt{{k^2}+1}}}{{3{k^2}+4}}$．
∵S_ACBD=$\frac{1}{2}$•|CD|•|y₁-y₂|=2|y₁-y₂|=$\frac{{24\sqrt{2}}}{7}$，
∴$\frac{{576（{k^2}+1）}}{{{{（3{k^2}+4）}^2}}}$=$\frac{576•2}{49}$，解得k=±1．
∴直线l的方程为x±y+1=0．

点评 本题考查了椭圆方程的求法，考查了直线与圆锥曲线位置关系的应用，灵活运用韦达定理解题是解决该题的关键，是中档题．