题目内容
已知函数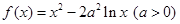 .
.
(1)若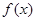 在
在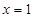 处取得极值,求实数
处取得极值,求实数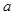 的值;
的值;
(2)求函数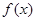 的单调区间;
的单调区间;
(3)若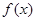 在
在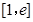 上没有零点,求实数
上没有零点,求实数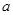 的取值范围.
的取值范围.
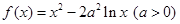 .
.(1)若
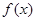 在
在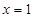 处取得极值,求实数
处取得极值,求实数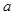 的值;
的值;(2)求函数
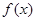 的单调区间;
的单调区间;(3)若
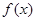 在
在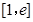 上没有零点,求实数
上没有零点,求实数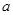 的取值范围.
的取值范围.(1)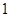 ;(2)单调递增区间为
;(2)单调递增区间为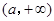 ,单调递减区间为
,单调递减区间为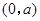 ;(3)
;(3)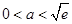 .
.
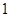 ;(2)单调递增区间为
;(2)单调递增区间为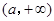 ,单调递减区间为
,单调递减区间为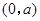 ;(3)
;(3)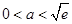 .
.试题分析:(1)求函数极值分四步,一是求函数定义域
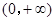 ,二是求函数导数
,二是求函数导数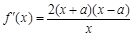 ,三是根据导数为零将定义区间分割,讨论导数值正负
,三是根据导数为零将定义区间分割,讨论导数值正负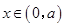 ,
,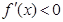 ;
;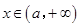 ,
, ,,四是根据导数符号变化确定极值点
,,四是根据导数符号变化确定极值点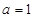 ;(2)利用导数求函数单调性,也是四个步骤.一是求出定义域:,二是求导数,三是分析导数符号变化情况,四是根据导数符号写出对应单调区间:减区间为
;(2)利用导数求函数单调性,也是四个步骤.一是求出定义域:,二是求导数,三是分析导数符号变化情况,四是根据导数符号写出对应单调区间:减区间为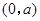 ,增区间
,增区间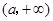 ; (3)
; (3)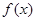 在
在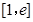 上没有零点,即
上没有零点,即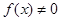 在
在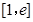 上恒成立,也就是
上恒成立,也就是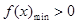 或
或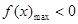 ,又
,又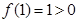 ,只须在区间
,只须在区间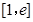 上
上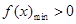 .以下有两个思路,一是求最小值,需分类讨论,当
.以下有两个思路,一是求最小值,需分类讨论,当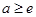 时,
时,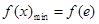 .当
.当 时,
时,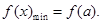 当
当 时,
时,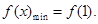 二是变量分离,
二是变量分离, ,只需求函数
,只需求函数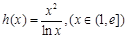 的最小值.
的最小值.试题解析:解:(1)
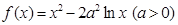 的定义域为
的定义域为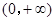 . 1分
. 1分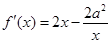
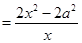
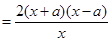 . 2分
. 2分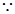
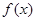 在
在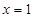 处取得极值,
处取得极值,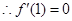 ,解得
,解得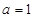 或
或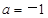 (舍). 3分
(舍). 3分当
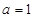 时,
时,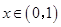 ,
,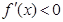 ;
;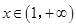 ,
, ,
,所以
 的值为
的值为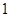 . 4分
. 4分(2)令
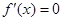 ,解得
,解得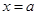 或
或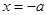 (舍). 5分
(舍). 5分当
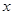 在
在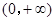 内变化时,
内变化时,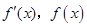 的变化情况如下:
的变化情况如下: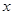 | 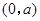 | 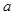 | 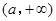 |
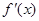 | 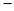 | 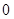 | 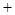 |
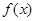 | ↘ | 极小值 | ↗ |
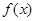 的单调递增区间为
的单调递增区间为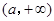 ,单调递减区间为
,单调递减区间为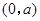 . 8分
. 8分(3)要使
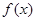 在
在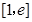 上没有零点,只需在
上没有零点,只需在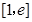 上
上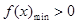 或
或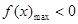 ,
,又
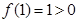 ,只须在区间
,只须在区间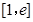 上
上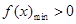 .
.(ⅰ)当
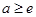 时,
时,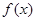 在区间
在区间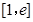 上单调递减,
上单调递减,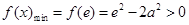 ,
,解得
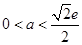 与
与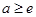 矛盾. 10分
矛盾. 10分(ⅱ) 当
 时,
时,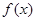 在区间
在区间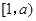 上单调递减,在区间
上单调递减,在区间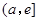 上单调递增,
上单调递增,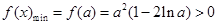 ,
,解得
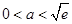 ,所以
,所以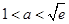 . 12分
. 12分(ⅲ)当
 时,
时,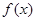 在区间
在区间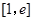 上单调递增,
上单调递增,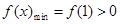 ,满足题意.
,满足题意.综上,
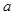 的取值范围为
的取值范围为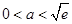 . 13分
. 13分
练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
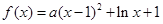 .
.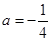 时,求函数
时,求函数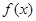 的极值;
的极值;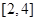 上是减函数,求实数
上是减函数,求实数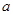 的取值范围;
的取值范围;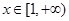 时,函数
时,函数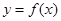 图像上的点都在
图像上的点都在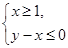 所表示的平面区域内,求实数
所表示的平面区域内,求实数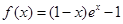 .
.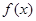 的最大值;
的最大值;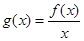 ,
,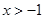 ,且
,且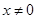 ,证明:
,证明: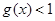 .
. 在区间
在区间 上取得最小值4,则
上取得最小值4,则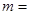 ___________.
___________.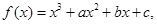 下列结论中①
下列结论中①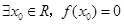 ②函数
②函数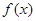 的图象是中心对称图形 ③若
的图象是中心对称图形 ③若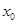 是
是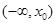 单调递减 ④若
单调递减 ④若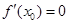 . 正确的个数有( )
. 正确的个数有( ) 的单调递增区间是_____________.
的单调递增区间是_____________. 的导函数为
的导函数为 ,若
,若 ,则
,则 .
.